Mathematik-Online-Lexikon: Skalarprodukt komplexer Vektoren

	[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
	Mathematik-Online-Lexikon:
	Skalarprodukt komplexer Vektoren

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Für Vektoren $x = (x_1,\dots,x_n)^{\operatorname t}, y = (y_1,\dots,y_n)^{\operatorname t}\in \mathbb{C}^n$ ist das kanonische Skalarprodukt durch

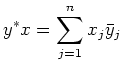
$\displaystyle y^*x = \sum_{j=1}^n x_j \bar y_j$

definiert mit der assoziierten Norm

$\displaystyle \vert z\vert = \sqrt{\vert z_1\vert^2 + \cdots + \vert z_n\vert^2}\, .$

Das Superskript bezeichnet dabei die Transposition und komplexe Konjugation eines Vektors.

Die Definition schließt den reellen Fall ein, bei dem die komplexe Konjugation entfällt.

automatisch erstellt am 25. 1. 2006