Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Dirichletproblem

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Eine zweifach differenzierbare Funktion $ \mbox{$h(x,y)$}$ von der offenen Menge $ \mbox{$G\subseteq \mathbb{R}^2 = \mathbb{C}$}$ nach $ \mbox{$\mathbb{R}$}$ heißt harmonisch, falls

$ \mbox{$\displaystyle \Delta h \; =\; h_{xx} + h_{yy}\; =\; 0\; . $}$
Sei $ \mbox{$f(z) = f(x + \mathrm{i}y) = u(x,y) + \mathrm{i}\, v(x,y)$}$ holomorph auf $ \mbox{$G$}$, geschrieben in Real- und Imaginärteil. Dann gelten die Cauchy-Riemannschen Differentialgleichungen
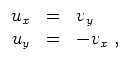
$ \mbox{$\displaystyle \begin{array}{rcl} u_x & = & v_y \\ u_y & = & -v_x\; , \\ \end{array}$}$
woraus $ \mbox{$u_{xx} = v_{yx} = v_{xy} = -u_{yy}$}$ und $ \mbox{$v_{xx} = -u_{yx} = -u_{xy} = -v_{yy}$}$ folgen. In anderen Worten, es gilt $ \mbox{$\Delta u = 0$}$ und $ \mbox{$\Delta v = 0$}$, d.h. sowohl der Real- als auch der Imaginärteil einer holomorphen Funktion sind harmonische Funktionen. Das kann man sich bei der Lösung von Gleichungen vom Typ $ \mbox{$\Delta h = 0$}$ mit vorgegebenen Randbedinungen zunutze machen.

Sei $ \mbox{$R > 0$}$, sei $ \mbox{$u_0:\partial B_R(0)\longrightarrow \mathbb{R}$}$ eine stetige Funktion. Gesucht ist eine stetige Funktion $ \mbox{$u: \bar{B}_R(0)\longrightarrow \mathbb{R}$}$ welche auf $ \mbox{$B_R(0)$}$ harmonisch ist, und welche der Randbedingung $ \mbox{$u\vert _{\partial B_R(0)} = u_0$}$ genügt.

Dieses Dirichletproblem hat als eindeutige Lösung die folgende Funktion. Sei $ \mbox{$x + \mathrm{i}y = r e^{\mathrm{i}\alpha}\in\mathbb{C}$}$, sei $ \mbox{$t\in\mathbb{R}$}$. Sei der Poissonkern gegeben durch

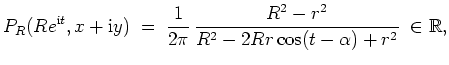
$ \mbox{$\displaystyle P_R(Re^{\mathrm{i}t},x+\mathrm{i}y)\; =\; \frac{1}{2\pi}\, \frac{R^2 - r^2}{R^2 - 2Rr\cos(t - \alpha) + r^2}\; \in\mathbb{R}, $}$
Dann ergibt sich unsere Lösung zu
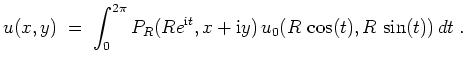
$ \mbox{$\displaystyle u(x,y)\; =\;\int_0^{2\pi} P_R(Re^{\mathrm{i}t},x + \mathrm{i}y)\, u_0(R\, \cos(t),R\, \sin(t))\, dt\; . $}$

Eine Möbiustransformation der oberen Halbebene $ \mbox{$\bar{H} = \{ (x,y)\in\mathbb{R}^2\; \vert\; y \geq 0\}$}$ auf den Einheitskreis liefert dazuhin folgende Aussage.

Sei $ \mbox{$g:\mathbb{R}\longrightarrow \mathbb{R}$}$ stetig mit $ \mbox{$\lim_{x\to -\infty} g(x) = \lim_{x\to +\infty} g(x) = g_0$}$. Dann ist die Dirichletsche Randwertaufgabe $ \mbox{$\Delta u = 0$}$ auf $ \mbox{$H$}$, $ \mbox{$u(x,0) = g(x)$}$ für $ \mbox{$x\in\mathbb{R}$}$, eindeutig durch

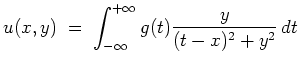
$ \mbox{$\displaystyle u(x,y) \; =\; \int_{-\infty}^{+\infty} g(t)\frac{y}{(t - x)^2 + y^2}\, dt $}$
lösbar.
(Autoren: Künzer/Meister/Nebe)

Beispiel:

[Verweise]
  automatisch erstellt am 25.  1. 2006