Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Residuenkalkül

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Das Residuenkalkül erlaubt es, die Berechnung von Integralen über hier der Einfachheit halber einfach geschlossene (ohne Überschneidungen) und gegen den Uhrzeigersinn orientierte Wege auf die Betrachtung der isolierten Singularitäten im Innern des Weges zurückzuführen.

Sei $ \mbox{$G\subseteq \mathbb{C}$}$ ein einfach zusammenhängendes Gebiet, seien $ \mbox{$z_1, \dots, z_n\in G$}$. Sei $ \mbox{$f:G\backslash \{ z_1,\dots,z_n\}\longrightarrow \mathbb{C}$}$ holomorph. Sei $ \mbox{$\gamma:[a,b]\longrightarrow G\backslash \{ z_1,\dots,z_n\}$}$ injektiv bis auf $ \mbox{$\gamma(a) = \gamma(b)$}$, und umlaufe $ \mbox{$\gamma$}$ die Punkte $ \mbox{$z_1$}$, ..., $ \mbox{$z_n$}$ in mathematisch positiver Richtung.

Entwickeln wir $ \mbox{$f$}$ um $ \mbox{$z_j$}$ in eine Laurentreihe, $ \mbox{$f = \sum_{k = -\infty}^\infty c_{j;k} (z-z_j)^k$}$ auf $ \mbox{$B_{R_j,0}(z_j)$}$, mit $ \mbox{$R_j > 0$}$ so, daß $ \mbox{$B_{R_j,0}(z_j)\subseteq G\backslash \{ z_1,\dots,z_n\}$}$. Man bezeichnet $ \mbox{$c_{j;-1}$}$ auch als das Residuum von $ \mbox{$f$}$ in $ \mbox{$z_j$}$, geschrieben $ \mbox{${\mbox{Res}}(f,z_j) := c_{j;-1}$}$. Dann gilt

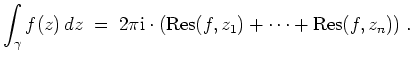
$ \mbox{$\displaystyle \int_\gamma f(z)\, dz\; =\; 2\pi \mathrm{i}\cdot ({\mbox{Res}}(f,z_1) + \cdots + {\mbox{Res}}(f,z_n))\; . $}$
Zur Berechnung dieser Residuen ist folgende Formel nützlich. Hat $ \mbox{$f$}$ in $ \mbox{$z_j$}$ einen Pol der Ordnung $ \mbox{$N$}$, so setzen wir $ \mbox{$g(z) := f(z)(z - z_j)^N$}$. Die Funktion $ \mbox{$g(z)$}$ ist nun holomorph auf die ungelochte Kreisscheibe $ \mbox{$B_{R_j}(z_j)$}$ fortsetzbar. Es gilt
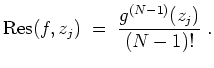
$ \mbox{$\displaystyle {\mbox{Res}}(f,z_j)\; =\; \frac{g^{(N-1)}(z_j)}{(N-1)!}\; . $}$
Anwendung findet der Residuensatz auch bei der Auswertung reeller Integrale. Hierzu lasse man $ \mbox{$\gamma$}$ ein Stück die reelle Achse entlanglaufen, und kehre über das Komplexe wieder zum reellen Ausgangangpunk zurück. Man lasse nun $ \mbox{$\gamma$}$ so variieren, daß in der Grenze der komplexe Anteil des Wegintegrals gegen Null geht. Dann kann man auf das Wegintegral den Residuensatz anwenden, und hat, wegen des verschwindenden komplexen Anteils, in der Tat das gefragte reelle Integral berechnet. Z.B. gilt folgendes:

Seien $ \mbox{$P(x)$}$, $ \mbox{$Q(x)$}$ reelle Polynome mit $ \mbox{${\mbox{Grad}}(Q)\geq{\mbox{Grad}}(P) + 2$}$. Sei $ \mbox{$Q(x)\neq 0$}$ für alle $ \mbox{$x\in\mathbb{R}$}$. Seien $ \mbox{$z_1$}$, ... $ \mbox{$z_n$}$ die komplexen Nullstellen von $ \mbox{$Q$}$ mit positivem Imaginärteil. Dann ist

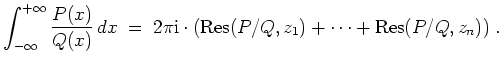
$ \mbox{$\displaystyle \int_{-\infty}^{+\infty} \frac{P(x)}{Q(x)}\, dx \; =\; 2\pi \mathrm{i}\cdot({\mbox{Res}}(P/Q,z_1) + \cdots + {\mbox{Res}}(P/Q,z_n))\; . $}$
(Autoren: Künzer/Meister/Nebe)

Beispiel:

[Verweise]
  automatisch erstellt am 25.  1. 2006