Mathematik-Online-Lexikon: Wahrscheinlichkeit

	[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
	Mathematik-Online-Lexikon:
	Wahrscheinlichkeit

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Übersicht

Ein Wahrscheinlichkeitsraum ist eine Menge von Elementarereignissen $\mbox{$\Omega$}$ , zusammen mit einer Menge $\mbox{${\cal{E}}$}$ an meßbaren Ereignissen von $\mbox{$\Omega$}$ , denen durch ein Maß $\mbox{$P$}$ (probability) eine Wahrscheinlichkeit für ihr Eintreten zugeordnet wird. Zwei Ereignisse schließen sich hierbei nicht aus, so z.B. treten in $\mbox{$\Omega = \{1, \dots, 6\}$}$ das Ereignis, daß man eine Zahl $\mbox{$\leq 3$}$ würfelt, und das Ereignis, daß man eine ungerade Zahl würfelt, genau dann beide ein, wenn $\mbox{$1$}$ oder $\mbox{$3$}$ fällt.

Formal haben wir also ein Tripel $\mbox{$(\Omega,{\cal{E}},P)$}$ , $\mbox{${\cal{E}}\subseteq {\operatorname{Pot}}(\Omega)$}$ , $\mbox{$P:{\cal{E}}\longrightarrow [0,1]$}$ , mit folgenden Eigenschaften.

$\mbox{$\Omega\in{\cal{E}}$}$ , $\mbox{$P(\Omega) = 1$}$ , d.h. das Ereignis $\mbox{$\Omega$}$ ist das sichere Ereignis.
Ist $\mbox{$A$}$ in $\mbox{${\cal{E}}$}$ , so ist auch $\mbox{$\Omega\backslash A$}$ in $\mbox{${\cal{E}}$}$ . Hierbei ist $\mbox{$P(A) + P(\Omega\backslash A) = 1$}$ , d.h. entweder tritt $\mbox{$A$}$ ein oder es tritt $\mbox{$A$}$ nicht ein. Insbesondere ist $\mbox{$\emptyset $}$ in $\mbox{${\cal{E}}$}$ , und $\mbox{$P(\emptyset ) = 0$}$ .
Sind $\mbox{$A$}$ und $\mbox{$B$}$ in $\mbox{${\cal{E}}$}$ , so sind auch $\mbox{$A\cap B$}$ und $\mbox{$A\cup B$}$ in $\mbox{${\cal{E}}$}$ . Es ist $\mbox{$P(A\cup B) = P(A) + P(B) - P(A\cap B)$}$ , d.h. eins von den Ereignissen $\mbox{$A$}$ oder $\mbox{$B$}$ tritt mit Wahrscheinlichkeit der Einzelereignisse ein, wovon die doppelt gezählte Wahrscheinlichkeit, daß beide eintreten, zu subtrahieren ist.
Sind $\mbox{$A_i$}$ , $\mbox{$i\in\mathbb{N}$}$ , in $\mbox{${\cal{E}}$}$ , so ist auch $\mbox{$\bigcup _{i\geq 1} A_i$}$ in $\mbox{${\cal{E}}$}$ . Sind die $\mbox{$A_i$}$ paarweise disjunkt, so ist $\mbox{$P(\bigcup _{i\geq 1} A_i) = \sum_{i\geq 1} P(A_i)$}$ .

Einelementige Teilmengen von $\mbox{$\Omega$}$ sind in der Regel meßbar, aber nicht immer. Es könnte, bei beliebigem $\mbox{$\Omega$}$ , z.B. $\mbox{${\cal{E}}= \{\emptyset ,\Omega\}$}$ sein.

Davon lassen sich folgende Begriffe ableiten. Sind $\mbox{$A$}$ und $\mbox{$B$}$ in $\mbox{${\cal{E}}$}$ , so heißt

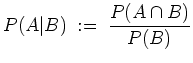
$\mbox{$\displaystyle P(A\vert B) \; :=\; \frac{P(A\cap B)}{P(B)} $}$

die bedingte Wahrscheinlichkeit von $\mbox{$A$}$ unter Voraussetzung von $\mbox{$B$}$ .

Es heißen die Ereignisse $\mbox{$A$}$ und $\mbox{$B$}$ in $\mbox{${\cal{E}}$}$ unabhängig, falls $\mbox{$P(A\cap B) = P(A)P(B)$}$ .

Allgemeiner heißen die Ereignisse $\mbox{$A_i$}$ in $\mbox{${\cal{E}}$}$ , $\mbox{$1\leq i\leq m$}$ , unabhängig, falls $\mbox{$P(A_{i_1}\cap\dots\cap A_{i_k}) = P(A_{i_1})\cdots P(A_{i_k})$}$ gilt für alle $\mbox{$1\leq i_1<i_2<\dots< i_k\leq m$}$ . Im Unterschied hierzu heißen diese Ereignisse paarweise unabhängig, falls nur $\mbox{$P(A_i\cap A_j) = P(A_i)P(A_j)$}$ stets gilt.

Der naheliegendste Wahrscheinlichkeitsraum im Falle endlich vieler Elementarereignisse $\mbox{$\Omega$}$ ist der Laplacesche Wahrscheinlichkeitsraum. Sei $\mbox{$n$}$ die Anzahl der Elemente in $\mbox{$\Omega$}$ , sei $\mbox{${\cal{E}}= {\operatorname{Pot}}(\Omega)$}$ , d.h. jeder Teilmenge von $\mbox{$\Omega$}$ werde eine Wahrscheinlichkeit für ihr Eintreten zugewiesen. Für $\mbox{$A\subseteq \Omega$}$ , welches $\mbox{$a$}$ Elemente enthalte, sei $\mbox{$P(A) = a/n$}$ . In anderen Worten, besteht ein Ereignis nur aus einem Elementarereignis, so ist seine Wahrscheinlichkeit $\mbox{$1/n$}$ .

(Autoren: Künzer/Meister/Nebe)

Beispiele:

[Verweise]

automatisch erstellt am 25. 1. 2006