Mathematik-Online-Lexikon: Korrelation und Kovarianz

	[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
	Mathematik-Online-Lexikon:
	Korrelation und Kovarianz

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Übersicht

Sind $\mbox{$X$}$ und $\mbox{$Y$}$ Zufallsvariablen, so heißt

$\mbox{$\displaystyle {\operatorname{Cov}}(X,Y) := {\operatorname{E}}\bigl((X-{\operatorname{E}}(X))(Y-{\operatorname{E}}(Y))\bigr) $}$

die Kovarianz von $\mbox{$X$}$ und $\mbox{$Y$}$ . Insbesondere ist $\mbox{${\operatorname{Cov}}(X,X)={\operatorname{Var}}(X)$}$ . Der Korrelationskoeffizient

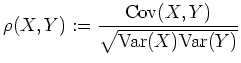
$\mbox{$\displaystyle \rho(X,Y) := \frac{{\operatorname{Cov}}(X,Y)}{\sqrt{{\operatorname{Var}}(X){\operatorname{Var}}(Y)}} $}$

von $\mbox{$X$}$ und $\mbox{$Y$}$ liegt im Intervall $\mbox{$[-1,1]$}$ . $\mbox{$X$}$ und $\mbox{$Y$}$ heißen unkorreliert, falls $\mbox{${\operatorname{Cov}}(X,Y) =0$}$ gilt.

Eigenschaften der Kovarianz

$\mbox{${\operatorname{Cov}}$}$ ist bilinear und symmetrisch, d.h.
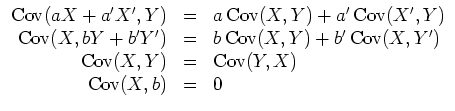
$\mbox{$\displaystyle \begin{array}{rcl} {\operatorname{Cov}}(aX + a'X' , Y)... ...torname{Cov}}(Y,X) \\ {\operatorname{Cov}}(X,b) & = & 0 \\ \end{array} $}$
für Zufallsvariablen $\mbox{$X, X', Y, Y'$}$ und reelle Zahlen $\mbox{$a,a',b,b'$}$ .
Unabhängige Zufallsvariablen sind stets unkorreliert, die Umkehrung hiervon gilt jedoch im allgemeinen nicht.
Es gilt $\mbox{$\vert\rho(X,Y)\vert = 1$}$ genau dann, wenn $\mbox{$a\in\mathbb{R}\backslash \{ 0\}$}$ und $\mbox{$b\in\mathbb{R}$}$ existieren mit
$\mbox{$\displaystyle P(X = aY + b) \; =\; 1\; . $}$
Sind $\mbox{$X$}$ und $\mbox{$Y$}$ unabhängige Zufallsvariablen, $\mbox{$X$}$ normalverteilt mit Verteilung $\mbox{$\Phi_{\mu,\sigma^2}$}$ , $\mbox{$Y$}$ normalverteilt mit Verteilung $\mbox{$\Phi_{\mu',\sigma'^2}$}$ , so wird für $\mbox{$c,d\in\mathbb{R}$}$ die Zufallsvariable $\mbox{$cX + dY$}$ normalverteilt mit Verteilung $\mbox{$\Phi_{c\mu + d\mu',\; c^2\sigma^2 + d^2\sigma'^2}$}$ . Ferner gilt, daß hier Unkorreliertheit und Unabhängigkeit äquivalent sind.

Eine zweidimensionale Stichprobe $\mbox{$(X_1,Y_1)$}$ , $\mbox{$(X_2,Y_2)$}$ ,..., $\mbox{$(X_n,Y_n)$}$ ( $\mbox{$n\geq 2$}$ ) besteht aus gleichverteilten Zufallsvariablen $\mbox{$X_1$}$ ,..., $\mbox{$X_n$}$ und $\mbox{$Y_1$}$ ,..., $\mbox{$Y_n$}$ und erfüllt folgende Unabhängigkeitsbedingung. Gegeben $\mbox{$c_i,d_i\in\mathbb{R}$}$ , so soll

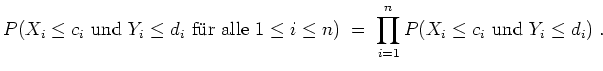
$\mbox{$\displaystyle P({\mbox{{$\mbox{$X_i\leq c_i$}$} und {$\mbox{$Y_i\leq d... ...= 1}^n P({\mbox{{$\mbox{$X_i\leq c_i$}$} und {$\mbox{$Y_i\leq d_i$}$}}})\; . $}$

Seien nun empirischer Mittelwerte $\mbox{$\bar X$}$ , $\mbox{$\bar Y$}$ , empirischer Varianzen $\mbox{$S^2_X$}$ , $\mbox{$S^2_Y$}$ und insbesondere empirische Kovarianz $\mbox{$S^2_{XY}$}$ und empirischer Korrelationskoeffizient wie folgt definiert. (Hierbei unterlassen wir es, den Index $\mbox{$n$}$ zu notieren.)

$\mbox{$\displaystyle \begin{array}{rcl} \bar X & := & \frac{1}{n}(\sum_{i = ... ...m}\\ \rho_{XY} & := & \frac{S_{XY}}{S_X S_Y} \;\in [-1,1] \\ \end{array}$}$

Die empirische Kovarianz ist ein erwartungstreuer Schätzer für die Kovarianz.

Für eine Realisierung $\mbox{$(x_1,y_1)$}$ , $\mbox{$(x_2,y_2)$}$ ,..., $\mbox{$(x,y)$}$ einer solchen zweidimensionalen Stichprobe schreiben wir entsprechend

$\mbox{$\displaystyle \begin{array}{rcl} \bar x & := & \frac{1}{n}(\sum_{i = ... ...}\\ \rho_{xy} & := & \frac{s_{xy}}{s_x s_y}\;\in [-1,1] . \\ \end{array}$}$

(Autoren: Künzer/Meister/Nebe)

Beispiel:

empirische Korrelation

[Verweise]

automatisch erstellt am 25. 1. 2006