Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Variationsrechnung (ohne Nebenbedingung)

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Problemstellung.

Variationsrechnung behandelt Extremalaufgaben auf Funktionenräumen. Anstatt nach dem Extremwert einer Funktion auf einem $ \mbox{$n$}$-dimensionalen Vektorraum zu fragen, wird nach dem Extremwert eines Funktionals auf einem Funktionenraum gefragt. Ein solches Funktional ist typischerweise eine physikalisch motivierte Größe, wie etwa die Länge des Graphen einer Funktion $ \mbox{$y$}$, oder die Höhe seines Schwerpunktes etc. Daher wird in der Regel ein Integral über einen von der Funktion  $ \mbox{$y$}$ abhängigen Ausdruck zu betrachten sein (welcher auch $ \mbox{$y'$}$, $ \mbox{$x$}$ etc. involvieren kann.)

Man reduziert dieses Problem auf eine Dimension - man legt eine beliebige Gerade $ \mbox{$y + \varepsilon v$}$ (im Funktionenraum !) durch die Kandidatenfunktion $ \mbox{$y$}$ und verlangt, daß die Ableitung nach $ \mbox{$\varepsilon $}$ des Funktionals, ausgewertet auf $ \mbox{$y + \varepsilon v$}$, bei $ \mbox{$\varepsilon = 0$}$ verschwindet. (Diese Idee stammt von Lagrange, welcher sich Lob von Euler dafür einhandelte.)

Genauer gesagt, die Extremalaufgabe ist zu lösen auf einer Teilmenge des Funktionenraums, spezifiziert durch Randbedingungen diverser Beschaffenheit, die wir im folgenden betrachten werden.

Rand beidseitig fixiert.

Sei $ \mbox{$y\in{\cal C}^2[x_0,x_1]$}$ eine zweifach stetig differenzierbare Funktion, welche die Randbedingungen $ \mbox{$y(x_0) = y_0$}$ und $ \mbox{$y(x_1) = y_1$}$ erfüllt. Sei $ \mbox{$F(x,y,y')$}$ ein Ausdruck in $ \mbox{$x$}$, $ \mbox{$y=y(x)$}$ und $ \mbox{$y'=y'(x)$}$. Zu lösen sei das Problem

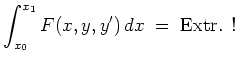
$ \mbox{$\displaystyle \int_{x_0}^{x_1} F(x,y,y')\, dx\; =\; {\mbox{Extr. !}} $}$
Sei dafür $ \mbox{$y + \varepsilon v$}$ eingesetzt wobei $ \mbox{$v$}$ zweimal stetig differenzierbar mit $ \mbox{$v(x_0) = 0$}$ und $ \mbox{$v(x_1) = 0$}$, aber ansonsten beliebig gewählt sein soll. Damit $ \mbox{$y$}$ den fraglichen Ausdruck (lokal) maximiert oder minimiert, muß die Ableitung dieses an $ \mbox{$y + \varepsilon v$}$ ausgewerteten Ausdrucks bei $ \mbox{$\varepsilon = 0$}$ verschwinden. In Zahlen heißt dies
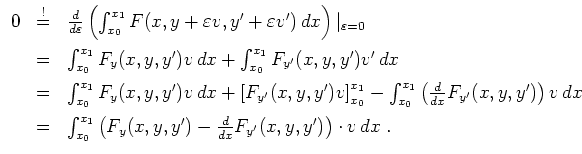
$ \mbox{$\displaystyle \begin{array}{rcl} 0 & \stackrel {!}{=} & \frac{d}{d\va... ...,y,y') - \frac{d}{dx} F_{y'}(x,y,y')\right)\cdot v \, dx\; . \\ \end{array}$}$
Da dies für alle Testfuntionen $ \mbox{$v$}$ gelten soll, muß die Euler-Lagrange-Differentialgleichung
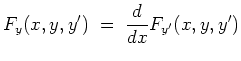
$ \mbox{$\displaystyle F_y(x,y,y') \; =\; \frac{d}{dx} F_{y'}(x,y,y') $}$
erfüllt sein.

Dies läßt sich noch umschreiben zu

$ \mbox{$\displaystyle F_y \; =\; F_{y'x} + y' F_{y'y} + y'' F_{y'y'} \; . $}$

Eine Lösung des Variationsproblems ist also auch eine Lösung dieser Differentialgleichung. Ist die Aufgabe sinnvoll gestellt, gilt das auch umgekehrt. D.h., man hat die Euler-Lagrange-Differentialgleichung zu lösen, um zu einer Lösung des Variationsproblems zu gelangen.

Rand beidseitig fixiert, $ \mbox{$F = F(y,y')$}$ unabhängig von $ \mbox{$x$}$.

Für den Fall, daß $ \mbox{$F = F(y,y')$}$ nicht von $ \mbox{$x$}$ abhängt, gilt

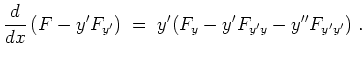
$ \mbox{$\displaystyle \frac{d}{dx}\left( F - y' F_{y'}\right)\; =\; y' (F_y - y' F_{y'y} - y'' F_{y'y'})\; . $}$
D.h. die integrierte Euler-Lagrange-Differentialgleichung
$ \mbox{$\displaystyle F - y' F_{y'}\; =\; {\mbox{const.}} $}$
liefert neben der Lösung $ \mbox{$y = {\mbox{const.}}$}$ die Lösungen der Euler-Lagrange-Differentialgleichung.

Rand einseitig fixiert.

Sei $ \mbox{$y\in{\cal C}^2[x_0,x_1]$}$, welche die einseitige Randbedingung $ \mbox{$y(x_0) = y_0$}$ erfüllt. Zu lösen sei das Problem

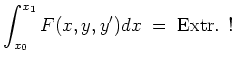
$ \mbox{$\displaystyle \int_{x_0}^{x_1} F(x,y,y') dx\; =\; {\mbox{Extr. !}} $}$
Sei dafür $ \mbox{$y + \varepsilon v$}$ eingesetzt, $ \mbox{$v$}$ zweimal stetig differenzierbar mit $ \mbox{$v(x_0) = 0$}$. Als Bedingung erhalten wir
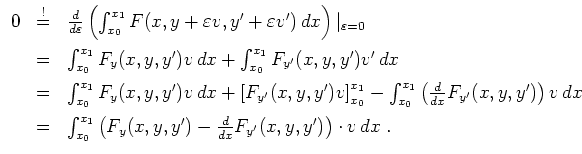
$ \mbox{$\displaystyle \begin{array}{rcl} 0 & \stackrel {!}{=} & \frac{d}{d\va... ...,y,y') - \frac{d}{dx} F_{y'}(x,y,y')\right)\cdot v \, dx\; . \\ \end{array}$}$
Da dies für alle Testfunktionen $ \mbox{$v$}$ gelten soll, muß die Euler-Lagrange-Differentialgleichung
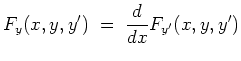
$ \mbox{$\displaystyle F_y(x,y,y') \; =\; \frac{d}{dx} F_{y'}(x,y,y') $}$
und dazuhin
$ \mbox{$\displaystyle F_{y'}(x_1,y(x_1),y'(x_1))\; =\; 0 $}$
gelten.

Transversale Randbedingung.

Sei $ \mbox{$y\in{\cal C}^2[x_0,x_1]$}$, welche links die Randbedingung $ \mbox{$y(x_0) = y_0$}$ und rechts die transversale Randbedingung $ \mbox{$y(x_1) = f(x_1)$}$ erfüllt, wobei der rechte Randpunkt $ \mbox{$x_1$}$ noch als variabel anzunehmen ist. Man kann sich vorstellen, daß der rechte Randpunkt der gesuchten Funktion auf der `Schiene' $ \mbox{$f(x)$}$ zu variieren ist.

Zu lösen sei wiederum das Problem

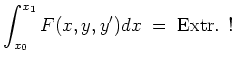
$ \mbox{$\displaystyle \int_{x_0}^{x_1} F(x,y,y') dx\; =\; {\mbox{Extr. !}} $}$
Sei dafür $ \mbox{$y + \varepsilon v$}$ eingesetzt, $ \mbox{$v$}$ zweimal stetig differenzierbar mit $ \mbox{$v(x_0) = 0$}$ und $ \mbox{$y(x_1) + \varepsilon v(x_1) = f(x_1)$}$. Bei fest gewählter Testfunktion $ \mbox{$v$}$ hängt $ \mbox{$x_1 = x_1(\varepsilon )$}$ also von $ \mbox{$\varepsilon $}$ ab. Insbesondere ist mit $ \mbox{$\dot x_1 = \frac{d}{d\varepsilon } x_1$}$
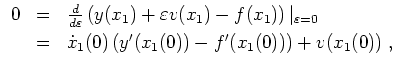
$ \mbox{$\displaystyle \begin{array}{rcl} 0 & = & \frac{d}{d\varepsilon } \lef... ... x_1(0) \left(y'(x_1(0)) - f'(x_1(0))\right) + v(x_1(0))\; , \\ \end{array}$}$
und also, mit den Abkürzungen $ \mbox{$x_1(0) =: x_{1,0}$}$, $ \mbox{$\dot x_1(0) =: \dot x_{1,0}$}$,
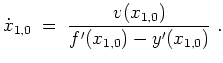
$ \mbox{$\displaystyle \dot x_{1,0}\; =\; \frac{v(x_{1,0})}{f'(x_{1,0}) - y'(x_{1,0})}\; . $}$

Als Bedingung erhalten wir so

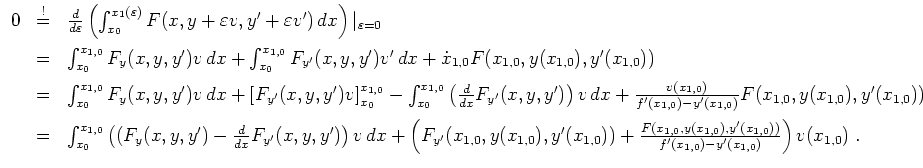
$ \mbox{$\displaystyle \begin{array}{rcl} 0 & \stackrel {!}{=} & \frac{d}{d\va... ...'(x_{1,0}))}{f'(x_{1,0}) - y'(x_{1,0})}\right) v(x_{1,0})\; .\\ \end{array}$}$
Da dies für alle Testfunktionen $ \mbox{$v$}$ gelten soll, muß die Euler-Lagrange-Differentialgleichung
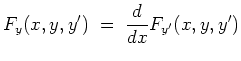
$ \mbox{$\displaystyle F_y(x,y,y') \; =\; \frac{d}{dx} F_{y'}(x,y,y') $}$
erfüllt sein, und die Transversalitätsbedingung
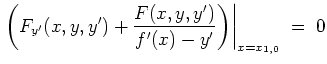
$ \mbox{$\displaystyle \left.\left(F_{y'}(x,y,y') + \frac{F(x,y,y')}{f'(x) - y'}\right)\right\vert _{x = x_{1,0}} \; =\; 0 $}$
gelten.
(Autoren: Künzer/Meister/Nebe)
[Beispiele] [Verweise]
  automatisch erstellt am 25.  1. 2006