Mathematik-Online-Lexikon: Laplace-Transformation

	[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
	Mathematik-Online-Lexikon:
	Laplace-Transformation

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Übersicht

Sei $\mbox{$c\in\mathbb{R}$}$ . Für eine Funktion $\mbox{$f:[0,\infty)\to\mathbb{R}$}$ mit $\mbox{$f\in O(\exp(ct))$}$ wird durch

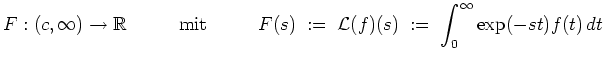
$\mbox{$\displaystyle F:(c,\infty)\to\mathbb{R}\hspace*{1cm}\text{ mit }\hspac... ... \;{\operatorname{\mathcal{L}}}(f)(s) \; :=\; \int_0^\infty\exp(-st)f(t)\,dt $}$

die Laplace-Transformierte von $\mbox{$f$}$ definiert. Etwas weiter gefaßt ist die komplexe Laplace-Transformierte durch

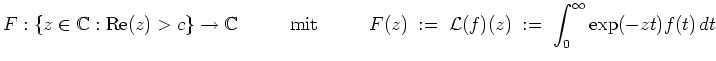
$\mbox{$\displaystyle F:\{z\in\mathbb{C}:{\operatorname{Re}}(z) > c\} \to\math... ...\;{\operatorname{\mathcal{L}}}(f)(z)\; :=\; \int_0^\infty\exp(- z t)f(t)\,dt $}$

definiert. Wir schreiben auch $\mbox{${\operatorname{\mathcal{L}}}(f(t)) := {\operatorname{\mathcal{L}}}(t\mapsto f(t)) = {\operatorname{\mathcal{L}}}(f)$}$ , d.h. wir zeichnen $\mbox{$t$}$ als Variable aus. Seien $\mbox{$f(t), g(t)$}$ aus $\mbox{$O(\exp(c t))$}$ , so schreiben wir auch $\mbox{$F := {\operatorname{\mathcal{L}}}(f)$}$ , $\mbox{$G := {\operatorname{\mathcal{L}}}(g)$}$ .

Das Faltungsprodukt von $\mbox{$f$}$ und $\mbox{$g$}$ ist als

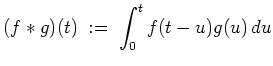
$\mbox{$\displaystyle (f\ast g)(t)\; :=\; \int_0^t f(t - u) g(u)\, du $}$

erklärt.

Die Laplace-Transformation hat folgende Eigenschaften.

$\mbox{$F(s)$}$ und $\mbox{$G(s)$}$ existieren für $\mbox{${\operatorname{Re}}(s) > c$}$ . Alle folgenden Aussagen beziehen sich auf diesen Bereich.
$\mbox{${\operatorname{\mathcal{L}}}(a f + b g ) = a F + b G$}$ für $\mbox{$a,b\in\mathbb{C}$}$ .
$\mbox{${\operatorname{\mathcal{L}}}(f(at))(s) = \frac{1}{a}{\operatorname{\mathcal{L}}}(f(t))(\frac{s}{a})$}$ für $\mbox{$a>0$}$ .
$\mbox{${\operatorname{\mathcal{L}}}(f(t+a))(s) = {\operatorname{\mathcal{L}}}(f_{\geq a})(s)\cdot \exp(as)$}$ für $\mbox{$a\geq 0$}$ , wobei $\mbox{$f_{\geq a}$}$ auf $\mbox{$[a,\infty)$}$ mit $\mbox{$f$}$ übereinstimme, und sonst den Wert $\mbox{$0$}$ annehme.
$\mbox{${\operatorname{\mathcal{L}}}(f'(t))(s) = s F(s) - f(0+)$}$ und $\mbox{${\operatorname{\mathcal{L}}}(\int_0^t f(u)\,du)(s) = \frac{1}{s} F(s)$}$ .
$\mbox{${\operatorname{\mathcal{L}}}(tf(t)) = - F'$}$ .
Falls $\mbox{$f(t)/t$}$ für $\mbox{$t\to 0$}$ einen Grenzwert annimmt, so ist $\mbox{${\operatorname{\mathcal{L}}}(\frac{1}{t}f(t))(s) = \int_s^\infty F(u)\, du$}$ , falls existent.
$\mbox{${\operatorname{\mathcal{L}}}(\exp(-at)f(t))(s) = F(s+a)$}$ für $\mbox{$a\in\mathbb{R}$}$ .
$\mbox{${\operatorname{\mathcal{L}}}(f\ast g) = F \cdot G$}$ .

Die Umkehrung der Laplace Transformation, d.h. die Bestimmung von $\mbox{$f$}$ mit $\mbox{${\operatorname{\mathcal{L}}}(f) = F$}$ bei gegebenem $\mbox{$F$}$ , ist unter geeigneten Voraussetzungen als

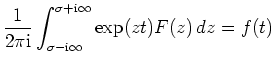
$\mbox{$\displaystyle \frac{1}{2\pi\mathrm{i}}\int_{\sigma-\mathrm{i}\infty}^{\sigma+\mathrm{i}\infty} \exp(z t)F(z)\, dz = f(t) $}$

bestimmbar, mit einem reellen, beliebig gewählten $\mbox{$\sigma > \max\{ 0,c\}$}$ . Das Integral $\mbox{$\int_{\sigma - \mathrm{i}\infty}^{\sigma + \mathrm{i}\infty}$}$ ist hierbei so zu verstehen, daß der Grenzwert über die Integrationswege $\mbox{$\gamma_r: [-1,1]\to\mathbb{C}: x\mapsto \sigma + \mathrm{i}rx$}$ für $\mbox{$r\to\infty$}$ zu bilden ist.

In der Praxis wird man angesichts dieses Ausdrucks eher versuchen, zunächst mit Hilfe obiger Eigenschaften die Laplace-Transformierte $\mbox{$F$}$ so umzuformen, daß $\mbox{$f$}$ unter Zuhilfenahme einer Tabelle gefunden werden kann.

Die Laplace-Transformation eignet sich zum Lösen von Differentialgleichungen, da sie Differentialoperationen in algebraische Operationen überführt, namentlich

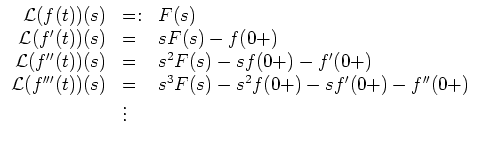
$\mbox{$\displaystyle \begin{array}{rll} {\operatorname{\mathcal{L}}}(f(t))(s... ...& s^3 F(s) - s^2 f(0+) - s f'(0+) - f''(0+) \\ & \vdots & \\ \end{array}$}$

Kann die transformierte Gleichung gelöst werden, so nach Rücktransformation auch die ursprüngliche.

(Autoren: Künzer/Meister/Nebe)

Beispiele:

[Verweise]

automatisch erstellt am 25. 1. 2006