Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] Englische Flagge
Mathematik-Online-Lexikon:

Mehrdimensionales Integral

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht
Das Integral einer stetigen Funktion $ f$ auf einem regulären Bereich $ V \subseteq \mathbb{R}^n$ kann als Grenzwert von Riemann-Summen definiert werden:

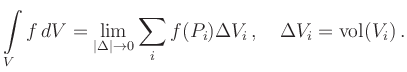
$\displaystyle \int\limits_V f\,dV = \lim_{\vert\Delta \vert\to 0} \sum_i f(P_i)\Delta V_i\,,\quad \Delta V_i=\operatorname{vol}(V_i) \,. $

Dabei wird $ V$ durch Vereinigungen disjunkter Elementarbereiche $ V_i$ (im allgemeinen Simplizes oder Parallelepipede) approximiert, d.h. der Hausdorff-Abstand von $ V$ und $ \bigcup\limits_i V_i$ strebt gegen 0. Mit $ \vert \Delta \vert$ wird der maximale Durchmesser der $ V_i$ bezeichnet, $ P_i$ sind beliebige Punkte in $ V_i$.

Die Schreibweise $ \Delta V_i \to dV$ symbolisiert den Grenzprozess, und $ dV$ nennt man das Volumenelement. Abkürzend schreibt man auch $ \int\limits_V f$ oder ausführlicher

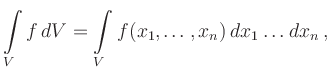
$\displaystyle \int\limits_V f \, dV = \int\limits_V f(x_1,\ldots,x_n)\,dx_1 \ldots dx_n\,, $

wenn man die Integrationsvariablen hervorheben will.

Aufgrund der Stetigkeit von $ f$ ist die Definition des Riemann-Integrals sowohl von der Wahl der Elementarbereiche $ V_{i}$ als auch der Punkte $ P_{i}$ unabhängig.

\includegraphics[width=0.5\moimagesize]{a_integral1}

Für eine positive Funktion entspricht das Integral dem Volumen der Menge

$\displaystyle \{(x_1,\ldots,x_n,h):\ 0\le h\le f(x),\,x\in V\} \,. $

Insbesondere ist $ \int\limits_V 1$ das Volumen des Integrationsbereiches $ V$.

Die Glattheitsvoraussetzungen an $ f$ und $ V$ können abgeschwächt werden, indem man das Integral über einen geeigneten Grenzprozess definiert. Man spricht dann von einem uneigentlichen Integral.

[Beispiele] [Verweise]
  automatisch erstellt am 22.  9. 2016