Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Residuenkalkül für rationale Integranden

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht
Für eine rationale Funktion $ f$ ohne reelle Polstellen und mit Zählergrad um mindestens $ 2$ kleiner als der Nennergrad gilt

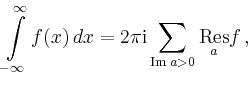
$\displaystyle \int\limits_{-\infty}^\infty f(x)\,dx = 2\pi\mathrm{i} \sum_{\operatorname{Im} a>0} \underset{a}{\operatorname{Res}} f \,, $

wobei die Residuen an allen Polstellen in der oberen Halbebene summiert werden.

Alternativ kann man über die Polstellen in der unteren Halbebene summieren. Dabei ändert sich aufgrund der entgegengesetzten Orientierung das Vorzeichen der Summe. Dies zeigt insbesondere, dass die Summe aller Residuen von $ f$ null ist.

siehe auch:

[Erläuterungen] [Beispiele]
  automatisch erstellt am 21. 11. 2013