Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Charakteristisches System einer partiellen Differentialgleichung

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht
Es wäre offensichtlich wünschenswert, wenn die $ x_i'$ mit den Koeffizienten der Ausgangsgleichung (*) übereinstimmen würden. Dies führt unmittelbar auf das autonome (hierzu geht ein, daß die PDG linear war) DGL - System

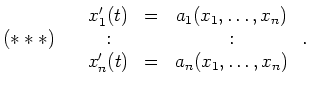
$\displaystyle (***) \ \ \ \ \begin{array}{ccc} x_1'(t) & = & a_1(x_1, \ldots , x_n) \\ : & & : \\ x_n'(t) & = & a_n(x_1, \ldots , x_n) \end{array} \ .$

Dieses System nennt man das charakteristische System der PDG und dessen Lösungen heißen Charakteristiken oder auch charakteristische Kurven der PDG.

Für sie gilt folgendes Lemma, das letztlich die Bedeutung der autonomen Systemen des vorhergehenden Abschnitts für partielle Differentialgleichungen darlegt und auch obige Überlegungen im Fall $ n = 2$ für die Ausgangsgleichung abschließt.

Lemma: Gegeben sei die lineare PDG 1.Ordnung

$\displaystyle (*) \ a_1(x_1, \ldots , x_n) y_{x_1} + \ldots + a_n(x_1, \ldots, x_n)y_{x_n} + a(x_1, \ldots, x_n)y + b(x_1, \ldots ,x_n) = 0 .$

Dann gilt:

$ y$ ist Lösung der zu gehörigen reduzierten Gleichung

$\displaystyle (**) \ a_1(x_1, \ldots , x_n) y_{x_1} + \ldots + a_n(x_1, \ldots, x_n)y_{x_n} = 0 .$

genau dann, wenn $ y$ ein erstes Integral des charakteristischen Systems der PDG ist.
(Aus: Vorlesungsskript HM3)

Erläuterung:

[Beispiele] [Verweise]
  automatisch erstellt am 25.  1. 2006