Mathematik-Online-Lexikon: Differentialoperatoren in Maple

	[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
	Mathematik-Online-Lexikon:
	Differentialoperatoren in Maple

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Übersicht

Den Gradienten einer skalaren Funktion

bezüglich der Koordinaten

erhält man in MAPLE mit dem Befehl grad(f,v). Man kann mit der Option coords den Gradienten auch in anderen als kartesischen Koordinaten berechnen lassen, insbesondere in Kugel- und Zylinderkoordinaten.

$\begin{maplegroup} \begin{mapleinput} \mapleinline{active}{1d}{with(linalg):}{% } \end{mapleinput}\par \end{maplegroup}$

$\begin{maplegroup} \begin{mapleinput} \mapleinline{active}{1d}{grad(3*cos(x) +... ...\mathrm{sin}(y)\,z] \end{displaymath} } \end{maplelatex}\par \end{maplegroup}$

$\begin{maplegroup} \begin{mapleinput} \mapleinline{active}{1d}{f := rho^2*cos(... ... \,2\,z \! \right] \end{displaymath} } \end{maplelatex}\par \end{maplegroup}$

$\begin{maplegroup} \begin{mapleinput} \mapleinline{active}{1d}{g := r^2*cos(th... ...rm{sin}(\theta ) ] \end{displaymath} } \end{maplelatex}\par \end{maplegroup}$

In MAPLE berechnet man die Divergenz eines Vektorfeldes bezüglich der Koordinaten mit dem Befehl diverge(f,v).

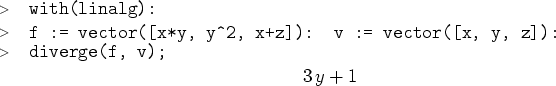
$\begin{maplegroup} \begin{mapleinput} \mapleinline{active}{1d}{with(linalg):}{... ...playmath} 3\,y + 1 \end{displaymath} } \end{maplelatex}\par \end{maplegroup}$

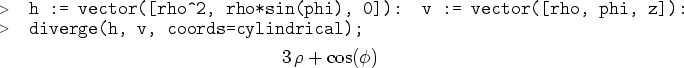
$\begin{maplegroup} \begin{mapleinput} \mapleinline{active}{1d}{h := vector([rh... ...\mathrm{cos}(\phi ) \end{displaymath} } \end{maplelatex}\par \end{maplegroup}$

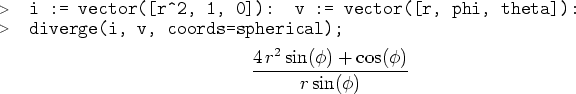
$\begin{maplegroup} \begin{mapleinput} \mapleinline{active}{1d}{i := vector([r^... ...thrm{sin}(\phi )}} \end{displaymath} } \end{maplelatex}\par \end{maplegroup}$

Die Rotation eines Vektorfeldes berechnet man in MAPLE mit dem Befehl curl(f,v). Wie bei dem Gradienten und der Divergenz lässt sich auch hier mit der Option coords die Rotation in anderen als kartesischen Koordinaten berechnen.

$\begin{maplegroup} \begin{mapleinput} \mapleinline{active}{1d}{with(linalg):}{% } \end{mapleinput}\par \end{maplegroup}$

$\begin{maplegroup} \begin{mapleinput} \mapleinline{active}{1d}{f := [x^2, y*z,... ...y, \, - y^{2}, \,0] \end{displaymath} } \end{maplelatex}\par \end{maplegroup}$

$\begin{maplegroup} \begin{mapleinput} \mapleinline{active}{1d}{g := [rho*sin(p... ...\rho }} \! \right] \end{displaymath} } \end{maplelatex}\par \end{maplegroup}$

$\begin{maplegroup} \begin{mapleinput} \mapleinline{active}{1d}{h := [r, r*cos(... ...(\phi ) \! \right] \end{displaymath} } \end{maplelatex}\par \end{maplegroup}$

(Autor: Marcus Reble)

[Verweise]

automatisch erstellt am 25. 1. 2006