Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Beispiel: Tschebyscheff vs äquidistante Interpolation

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht
Der Fehler bei polynomialer Interpolation kann stark von der Wahl der Stützstellen abhängen. Die einfache äquidistante Verteilung wird erheblich verbessert, wenn man als Stützstellen die Nullstellen der sogenannten Tschebyscheff-Polynome verwendet, die für $ x \in [-1,1]$ durch

$\displaystyle T_n(x) = \cos(n \arccos x) $

definiert sind. Die Nullstellen von $ T_{n+1}$,

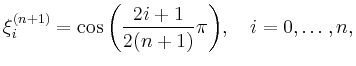
$\displaystyle \xi_i^{(n+1)}=\displaystyle{\cos \left ( \frac{2i+1}{2(n+1)} \pi \right )}, \quad i=0,\dots, n, $

heißen Tschebyscheff-Knoten auf dem Intervall $ [-1,1]$. Sie können mittels folgender Transformation auf ein beliebiges Intervall $ [a,b]$ überführt werden:

$\displaystyle x_i^{(n+1)} = a + \frac{(b - a)}{2}( \xi_i^{(n+1)} + 1). $

Die Abbildung zeigt die Tschebyscheff-Knoten für verschiedene $ n$. Es wird deutlich, dass die Knoten auf einer äquidistanten Winkelunterteilung basieren. Dies bewirkt eine höhere Knotendichte an den Intervallrändern.

\includegraphics[width=.33\linewidth]{chebknot_4}          \includegraphics[width=.33\linewidth]{chebknot_8}          \includegraphics[width=.33\linewidth]{chebknot_12}

Die folgenden Abbildungen vergleichen äquidistante (gestrichelt) und Tschebyscheff-Interpolation (gepunktet) für die Funktion $ f(x) = 1/(1+25x^2)$ (durchgezogene Linie) für Polynomgrad $ n = 4,8,12$.

\includegraphics[width=0.33\linewidth]{Tscheby_vs_Aequis_1_Bild1.eps}          \includegraphics[width=0.33\linewidth]{Tscheby_vs_Aequis_1_Bild3.eps}          \includegraphics[width=0.33\linewidth]{Tscheby_vs_Aequis_1_Bild5.eps}

Die Überlegenheit der Tschebyscheff-Knoten wird durch Plots der Interpolationsfehler noch deutlicher. Man erkennt, dass der Fehler am Rand des Intervalls bei der äquidistanten Stützstellenwahl für wachsende $ n$ immer größer wird, während er für die Tschebyscheff-Knoten stetig abnimmt und auf $ [-1,1]$ ungefähr gleich verteilt ist.

\includegraphics[height=3.3cm]{Tscheby_vs_Aequis_2_Bild1.eps}      \includegraphics[height=3.3cm]{Tscheby_vs_Aequis_2_Bild2.eps}      \includegraphics[height=3.3cm]{Tscheby_vs_Aequis_2_Bild3.eps}
\includegraphics[height=3.3cm]{Tscheby_vs_Aequis_2_Bild4.eps}      \includegraphics[height=3.3cm]{Tscheby_vs_Aequis_2_Bild5.eps}      \includegraphics[height=3.3cm]{Tscheby_vs_Aequis_2_Bild6.eps}

(Autoren: Wohlmuth/Hager)

siehe auch:

  automatisch erstellt am 29.  4. 2010