Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Beispiel: Robotorarm

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht
Die folgende Abbildung zeigt einen zweidimensionalen, zweiarmigen Roboterarm.

\begin{picture}(6.5,10)\linethickness{1.0mm} \put(2,1){\line(0,1){8}} \put(2,... ...,1){\oval(2,2)[tr]} \put(2.3,8.4){$\beta$} \put(2.3,1.2){$\alpha$} \end{picture}

Für einen beliebigen erreichbaren Zielpunkt $ P=\left( p_1,p_2 \right)$ sollen die Gelenkwinkel $ \alpha$ und $ \beta$ bestimmt werden. Dazu werden die Koordinaten $ p_i$ als Funktion der Winkel und der Armlängen $ a$ und $ b$ ausgedrückt.

Man erhält zunächst die Koordinaten des Punktes $ Q = (q_1, q_2)$ als

$\displaystyle q_1$ $\displaystyle = a \cos \alpha$    
$\displaystyle q_2$ $\displaystyle = a \sin \alpha$    

und dann

$\displaystyle p_1$ $\displaystyle = q_1 + b \cos (\beta - (\pi - \alpha)) = q_1 + b \cos(\alpha + \beta - \pi)$    
  $\displaystyle = a \cos \alpha - b \cos(\alpha + \beta),$    
$\displaystyle p_2$ $\displaystyle = a \sin \alpha - b \sin(\alpha + \beta).$    

Dieses zweidimensionale lineare Gleichungssystem kann mit dem Newton-Verfahren gelöst werden. Man setzt dazu $ \gamma = \alpha + \beta$ und schreibt das System in der Standardform

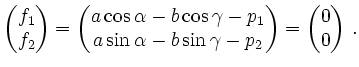
$\displaystyle \begin{pmatrix} f_1\\ f_2 \end{pmatrix} = \begin{pmatrix} a \co... ...- b \sin \gamma - p_2 \end{pmatrix} = \begin{pmatrix} 0\\ 0 \end{pmatrix}\,. $

Mit der Jacobi-Matrix

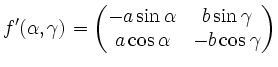
$\displaystyle f^\prime (\alpha,\gamma) = \begin{pmatrix} -a \sin \alpha & b \sin \gamma \\ a \cos \alpha & -b \cos \gamma \end{pmatrix}$

läuft ein Verfahrensschritt $ (\alpha,\gamma) \to (\alpha\,^\prime,\gamma\,^\prime)$ folgendermaßen ab:

Man löst das lineare Gleichungssystem

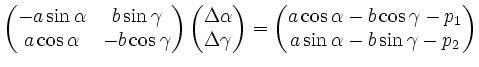
$\displaystyle \begin{pmatrix} -a \sin \alpha & b \sin \gamma \\ a \cos \alpha ... ...s \alpha -b \cos \gamma -p_1\\ a \sin \alpha -b \sin \gamma -p_2 \end{pmatrix}$

und setzt

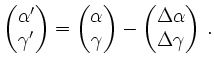
$\displaystyle \begin{pmatrix} \alpha^\prime\\ \gamma^\prime \end{pmatrix}= \be... ...\end{pmatrix}- \begin{pmatrix} \Delta \alpha\\ \Delta \gamma \end{pmatrix}\,. $

Der Schritt ist für alle $ ( \alpha , \gamma )$ mit

$\displaystyle \det f^\prime (\alpha, \gamma) = ab ( \sin \alpha \cos \gamma -\c... ...in \gamma) \neq 0 \quad \Longleftrightarrow \quad \tan \alpha \neq \tan \gamma $

durchführbar, d.h. $ \beta = \gamma - \alpha \neq 0 ,\, \pi$ .
(Autoren: Hager/Wohlmuth)

siehe auch:

  automatisch erstellt am 9.  6. 2006