Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Lineares Gleichunssystem

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Bestimme die Lösungsmenge des folgenden reellen Gleichungssystems.

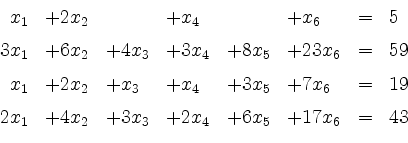
\begin{displaymath} \begin{array}{rlllllcl} x_1 &+2x_2& &+x_4 & &+x_6 &=& 5\vspa... ...m}\\ 2x_1 &+4x_2&+3x_3 &+2x_4 &+6x_5&+17x_6 &=& 43 \end{array}\end{displaymath}

Lösung.

Wir schreiben das Gleichungssystem in Matrixform $ Ax=b$ , und wenden den Gaußschen Algorithmus auf die erweiterte Matrix $ (A\vert b)$ an. Es wird

\begin{displaymath} \begin{array}{rl} &\left(\begin{array}{rrrrrr\vert l} 1& 2... ... 1& 3\\ 0& 0& 0& 0& 0& 0& 0 \end{array}\right)\;. \end{array}\end{displaymath}

Die ausgewählten Spalten sind $ k_1 = 1$ , $ k_2 = 3$ und $ k_3 = 5$ . Die nicht ausgewählten Spalten sind $ k'_1 = 2$ , $ k'_2 = 4$ und $ k'_3 = 6$ .

Eine partikuläre Lösung ist (durch positives Einfüllen)

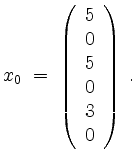
$\displaystyle x_0 \; =\; \left(\begin{array}{r}5\\ 0\\ 5\\ 0\\ 3\\ 0\end{array}\right)\;. $

Lösungen des zugehörigen homogenen Gleichungssystems sind also (durch negatives Einfüllen)

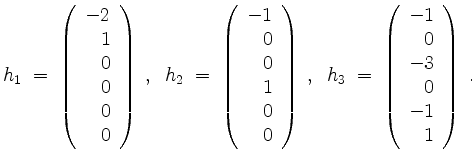
$\displaystyle h_1 \; =\; \left(\begin{array}{r} -2\\ 1\\ 0\\ 0\\ 0\\ 0\end{arra... ...3 \; =\; \left(\begin{array}{r} -1\\ 0\\ -3\\ 0\\ -1\\ 1\end{array}\right)\; . $

Die Lösungsmenge des Gleichungssystems ist also

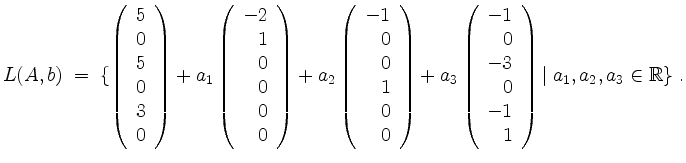
$\displaystyle L(A,b) \;=\; \{ \left(\begin{array}{r} 5\\ 0\\ 5\\ 0\\ 3\\ 0\end... ...\\ 0\\ -3\\ 0\\ -1\\ 1\end{array}\right) \vert\; a_1,a_2,a_3\in\mathbb{R}\}\;. $

(Autoren: Künzer/Martin/Tentler/Wahrheit)

siehe auch:

  automatisch erstellt am 11.  8. 2006