Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Basisergänzung, Basisauswahl

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht
  1. Untersuche das folgende Tupel von Vektoren in $ V=\mathbb{R}^4$ auf lineare Unabhängigkeit. Ergänze es gegebenfalls zu einer Basis.

    $\displaystyle ( \left(\begin{array}{r} 1\\ 0\\ 1\\ 0\end{array}\right),\; \left... ...\end{array}\right),\; \left(\begin{array}{r} 1\\ 3\\ 1\\ 0\end{array}\right) ) $

  2. Zeige, daß das folgende Tupel ein linear abhängiges Erzeugendensystem von $ \mathbb{R}^4$ ist. Wähle aus ihm eine Basis des $ \mathbb{R}^4$ aus.

    $\displaystyle ( \left(\begin{array}{r} 1\\ 2\\ 3\\ 3\end{array}\right),\; \left... ...\end{array}\right),\; \left(\begin{array}{r} 1\\ 0\\ 1\\ 0\end{array}\right) ) $

Lösung.

  1. Wir berechnen eine Zeilenstufenform.

    \begin{displaymath} \begin{array}{rl} & \left(\begin{array}{rrrrrrr} 1 & 1 & 1... ... 0 & 1 & 0 & -1 & 0 \\ \end{array}\right) \; . \\ \end{array}\end{displaymath}

    Da die ersten drei Spalten ausgewählt sind, liegt in der Aufgabenstellung in der Tat ein linear unabhängiges Tupel vor.

    Da dazuhin die vierte Spalte ausgewählt ist, ist

    $\displaystyle (\;\begin{pmatrix}1\\ 0\\ 1\\ 0\end{pmatrix},\; \begin{pmatrix}1\... ...ix}1\\ 3\\ 1\\ 0\end{pmatrix},\; \begin{pmatrix}1\\ 0\\ 0\\ 0\end{pmatrix} \;) $

    eine Basisergänzung zu einer Basis von $ \mathbb{R}^4$ .

  2. Wegen $ \dim\mathbb{R}^4=4$ muß dieses Tupel von Vektoren linear abhängig sein. Zur Auswahl einer Basis des davon erzeugten Unterraums bringen wir die folgende Matrix auf Zeilenstufenform.

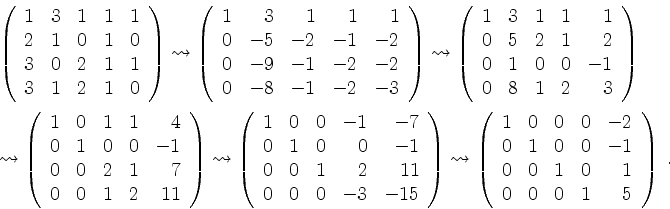
    \begin{displaymath} \begin{array}{l} \left(\begin{array}{rrrrr} 1& 3& 1& 1& 1\\ ... ... 0& 1& 0& 1\\ 0& 0& 0& 1& 5 \end{array}\right)\;. \end{array}\end{displaymath}

    Da hierin nicht alle Spalten ausgewählt sind, bestätigt diese Rechnung die lineare Abhängigkeit.

    Ferner bildet das Tupel der ersten vier Vektoren

    $\displaystyle ( \left(\begin{array}{r} 1\\ 2\\ 3\\ 3\end{array}\right),\; \left... ...\end{array}\right),\; \left(\begin{array}{r} 1\\ 1\\ 1\\ 1\end{array}\right) ) $

    eine Basis des von ihm erzeugten Unterraums, der aus Dimensionsgründen gleich dem $ \mathbb{R}^4$ ist.

(Autoren: Künzer/Martin/Tentler/Wahrheit)
[Verweise]
  automatisch erstellt am 11.  8. 2006