
Mathematik-Online-Lexikon:

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online-Lexikon: | |
Darstellungsmatrix, Kern und Bild |
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z | Übersicht |
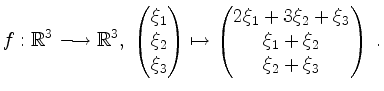
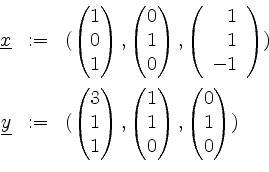
Basen des
Lösung.
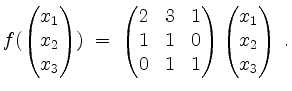
Eine Abbildung dieser Form ist stets linear.
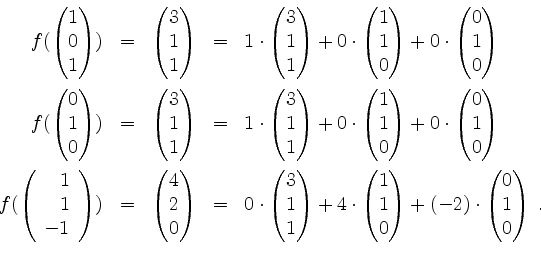
Also ist
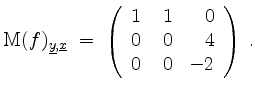
Ferner wird
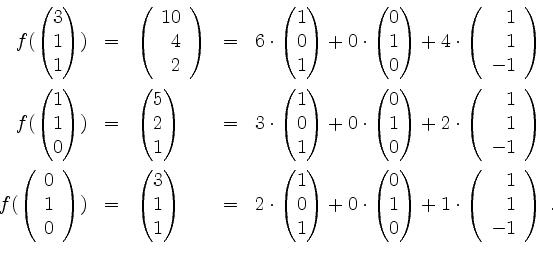
Also ist
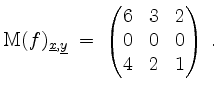
Alternativ. Es wird
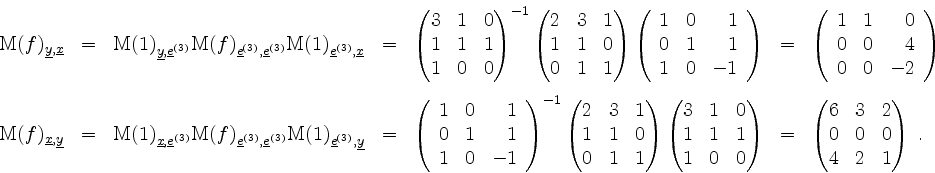
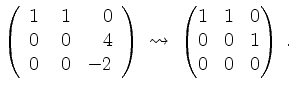
Also ist
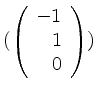 eine Basis von
eine Basis von
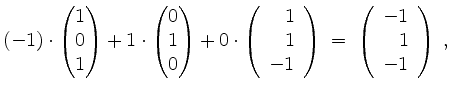
und somit ist
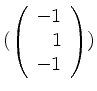 eine Basis von
eine Basis von
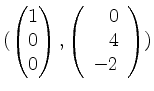 eine Basis von
eine Basis von
Es ist
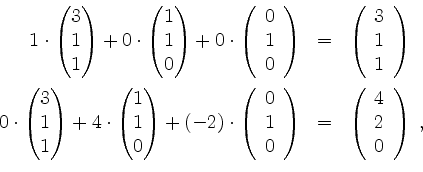
und somit ist
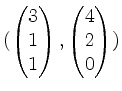 eine Basis von
eine Basis von
| automatisch erstellt am 22. 8. 2006 |