Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Rang von Matrixpotenzen

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Sei

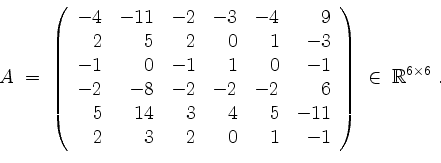
\begin{displaymath} A \;=\; \left( \begin{array}{rrrrrr} -4 & -11 & -2 & -3 & -... ...& -1 \\ \end{array}\right) \;\in\; \mathbb{R}^{6\times 6}\; . \end{displaymath}

1.
Bestimme den Rang von $ A$ , $ A^2$ , $ A^3$ und $ A^4$ .
2.
Sei $ K$ ein Körper, sei $ n\geq 1$ , und sei $ B\in K^{n\times n}$ . Zeige, daß es ein $ k\geq 0$ gibt mit $ \operatorname{Rang}(B^l) = \operatorname{Rang}(B^k)$ für alle $ l\geq k$ .
3.
Sei $ B$ wie in 2.. Sei $ k\geq 0$ . Zeige, daß aus $ \operatorname{Rang}(B^{k+1}) = \operatorname{Rang}(B^k)$ bereits folgt, daß $ \operatorname{Rang}(B^l) = \operatorname{Rang}(B^k)$ für alle $ l\geq k$ .
4.
Sei $ B$ wie in 2., und seien $ k,\, l\,\geq\, 0$ . Zeige, daß aus $ \operatorname{Rang}(B^l) = \operatorname{Rang}(B^k)$ folgt, daß die Zeilenstufenformen von $ B^l$ und $ B^k$ übereinstimmen.

Lösung.

1.
Die Zeilenstufenform von $ A$ berechnet sich unter Vernachlässigung von Nullzeilen zu

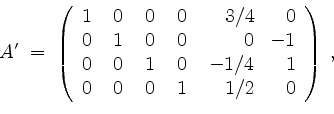
\begin{displaymath} A' \;=\; \left( \begin{array}{rrrrrr} 1 & \; 0 & \; 0 & \; ... ...4 & 1 \\ 0 & 0 & 0 & 1 & 1/2 & 0 \\ \end{array}\right) \; , \end{displaymath}

und somit ist $ \operatorname{Rang} A = 4$ .

Die Matrix $ A'$ ist (bis auf Weglassen von Nullzeilen) durch Multiplikation von A mit einer invertierbaren Matrix von links hervorgegangen. Somit haben $ A^2$ und

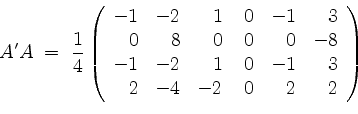
\begin{displaymath} A'A \;=\; \frac{1}{4} \left( \begin{array}{rrrrrr} -1 & -2 ... ...0 & -1 & 3 \\ 2 & -4 & -2 & 0 & 2 & 2 \\ \end{array}\right) \end{displaymath}

dieselbe Zeilenstufenform, nämlich, unter Vernachlässigung von Nullzeilen,

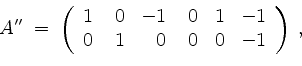
\begin{displaymath} A'' \;=\; \left( \begin{array}{rrrrrr} 1 & \; 0 & -1 & \; 0 & 1 & -1 \\ 0 & 1 & 0 & 0 & 0 & -1 \\ \end{array}\right) \; , \end{displaymath}

und somit ist $ \operatorname{Rang}\!(A^2) = 2$ .

Es haben $ A^3$ und

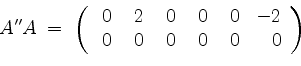
\begin{displaymath} A'' A \;=\; \left( \begin{array}{rrrrrr} \; 0 & \; 2 & \; 0 ... ... & \; 0 & -2 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array}\right) \end{displaymath}

dieselbe Zeilenstufenform, nämlich, unter Vernachlässigung von Nullzeilen,

\begin{displaymath} A''' \;=\; \left( \begin{array}{rrrrrr} 0 & 1 & 0 & 0 & 0 & -1 \\ \end{array}\right) \; , \end{displaymath}

und somit ist $ \operatorname{Rang}\!(A^3) = 1$ .

Es haben $ A^4$ und

\begin{displaymath} A''' A \;=\; \left( \begin{array}{rrrrrr} \; 0 & \; 2 & \; 0 & \; 0 & \; 0 & -2 \\ \end{array}\right) \end{displaymath}

dieselbe Zeilenstufenform, nämlich, unter Vernachlässigung von Nullzeilen,

\begin{displaymath} A'''' \;=\; \left( \begin{array}{rrrrrr} 0 & 1 & 0 & 0 & 0 & -1 \\ \end{array}\right) \; , \end{displaymath}

und somit ist $ \operatorname{Rang}\!(A^4) = 1$ .

2.
Wegen $ \operatorname{Bild}(B^{m+1}) \subseteq \operatorname{Bild}(B^m)$ ist die Folge $ (\operatorname{Rang}(B^m))_{m\geq 0}$ monoton fallend. Da sie aus nichtnegativen ganzen Zahlen besteht, wird sie konstant ab einem $ k\geq 0$ .
3.
Ist $ \operatorname{Rang}(B^k) = \operatorname{Rang}(B^{k+1})$ , so ist $ \operatorname{Bild}(B^k) = \operatorname{Bild}(B^{k+1})$ . Wir haben zu zeigen, daß für $ m\geq 0$ auch $ \operatorname{Bild}(B^{k+m}) = \operatorname{Bild}(B^{k+m+1})$ ist.

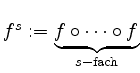Sei $ f:K^n\longrightarrow K^n$ , $ x\mapsto Bx$ . Sei $ f^s:=\underbrace{f\circ\cdots\circ f}_{s\rm -fach}$ für $ s\geq 0$ . Insbesondere ist $ \operatorname{Bild}(f^s)=\operatorname{Bild}(B^s)$ .

Aus $ \operatorname{Bild}(f^k) = \operatorname{Bild}(f^{k+1})$ folgt

$\displaystyle \operatorname{Bild}(f^{k+m}) \;=\; f^m(\operatorname{Bild}(f^k)) \;=\; f^m(\operatorname{Bild}(f^{k+1})) \;=\; \operatorname{Bild}(f^{k+m+1}) \;. $

4.
Nehmen wir $ k\leq l$ an. Es genügt mit Transposition, die Aussage für die Spaltenstufenformen zu zeigen. Dabei sei eine Matrix in Spaltenstufenform, wenn ihre Transponierte in Zeilenstufenform ist.

Sei $ r=\operatorname{Rang}(B^l)$ . Sei $ U\in K^{n\times r}$ die Spaltenstufenform von $ B^k$ nach Streichung aller Nullspalten. Sei $ V\in K^{n\times r}$ die Spaltenstufenform von $ B^l$ nach Streichung aller Nullspalten.

Sowohl die Spalten von $ U$ als auch die Spalten von $ V$ bilden eine Basis von $ \operatorname{Bild}(B^l)=\operatorname{Bild}(B^k)$ (vgl. Beweis zu 3.).

Also gibt es eine invertierbare Matrix $ S\in K^{r\times r}$ so, daß $ US=V$ . Da $ U$ und $ V$ sich in Spaltenstufenform befinden und keine Nullspalten enthalten, folgt $ S = \mathrm{E}_r$ und $ U = V$ .

(Autoren: Künzer/Martin/Tentler/Wahrheit)

siehe auch:

  automatisch erstellt am 22.  8. 2006