Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Eine Jordanform

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Es sei

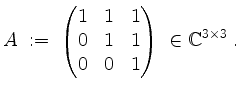
$\displaystyle A \;:=\; \begin{pmatrix}1&1&1\\ 0&1&1\\ 0&0&1\end{pmatrix}\;\in\mathbb{C}^{3\times 3} \;. $

1.
Ist $ A$ diagonalisierbar?
2.
Berechne eine invertierbare Matrix $ S\in\mathbb{C}^{3\times 3}$ und eine Matrix $ J\in\mathbb{C}^{3\times 3}$ in Jordanform so, daß $ S^{-1}AS=J$ .
3.
Berechne das Minimalpolynom von $ A$ .

Lösung.

Wir berechnen zunächst das charakteristische Polynom von $ A$ .

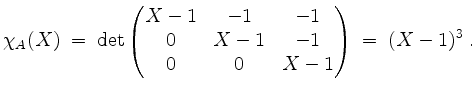
$\displaystyle \chi_A(X) \;=\; \det\begin{pmatrix}X-1&-1&-1\\ 0&X-1&-1\\ 0&0&X-1\end{pmatrix} \;=\; (X-1)^3\;. $

Damit haben wir einen Eigenwert $ \lambda=1$ mit algebraischer Vielfachheit $ 3$ .

Zur Berechnung der Matrizen $ S$ und $ J$ setzen wir

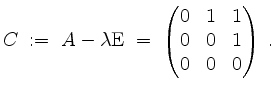
$\displaystyle C \;:=\; A-\lambda\mathrm{E} \;=\; \begin{pmatrix}0&1&1\\ 0&0&1\\ 0&0&0\end{pmatrix} \;. $

Der zugehörige Eigenraum ergibt sich zu

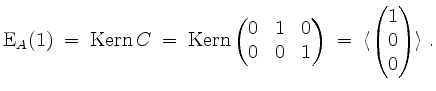
$\displaystyle \mathrm{E}_A(1) \;=\; \operatorname{Kern }C \;=\; \operatorname{K... ...&0&1\end{pmatrix} \;=\; \langle\begin{pmatrix}1\\ 0\\ 0\end{pmatrix}\rangle\;. $

Die geometrische Vielfachheit des Eigenwerts $ 1$ ist somit $ \dim\mathrm{E}_A(1)=1$ .

Die Matrix $ A$ ist nicht diagonalisierbar, denn die geometrische Vielfachheit des Eigenwerts ist kleiner als seine algebraische Vielfachheit.

Weiter wird

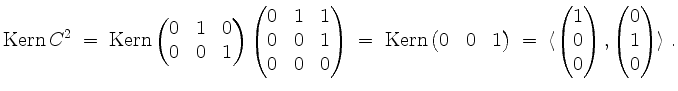
$\displaystyle \operatorname{Kern }C^2 \;=\; \operatorname{Kern } \begin{pmatrix... ...pmatrix}1\\ 0\\ 0\end{pmatrix},\begin{pmatrix}0\\ 1\\ 0\end{pmatrix}\rangle\;. $

Schließlich wird

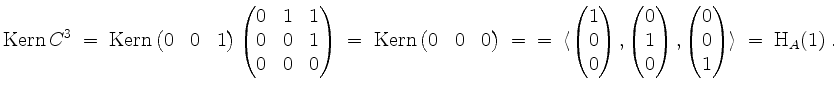
$\displaystyle \operatorname{Kern }C^3 \;=\; \operatorname{Kern }\begin{pmatrix}... ...pmatrix},\begin{pmatrix}0\\ 0\\ 1\end{pmatrix}\rangle \;=\; \mathrm{H}_A(1)\;. $

Also sieht unser Tableau vor der Bildung von Ketten wie folgt aus.

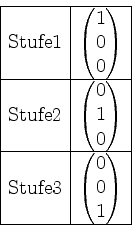
\begin{displaymath} \begin{array}{\vert l\vert l\vert}\hline \mathrm{Stufe } 1 &... ... 3 & \begin{pmatrix}0\\ 0\\ 1\end{pmatrix}\\ \hline \end{array}\end{displaymath}

Nun bilden wir alle Vektoren in Stufe $ 3$ mittels der Matrix $ C$ ab, fügen sie in Stufe $ 2$ ein, und streichen von den schon vorhandenen Vektoren in Stufe $ 2$ eine geeignete Auswahl, so daß das Tableau weiterhin in Stufe $ 1$ und Stufe $ 2$ eine Basis von $ \operatorname{Kern}(C^2)$ enthält. In diesem Fall muß aus Dimensionsgründen der schon vorhandene Vektor aus Stufe $ 2$ gestrichen werden.

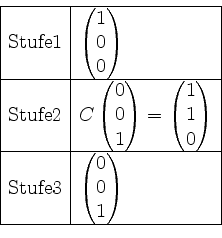
\begin{displaymath} \begin{array}{\vert l\vert l\vert}\hline \par \mathrm{Stufe ... ...3 & \begin{pmatrix}0\\ 0\\ 1\end{pmatrix} \\ \hline \end{array}\end{displaymath}

Schließlich bilden wir alle Vektoren in Stufe $ 2$ mittels der Matrix $ C$ ab, fügen sie in Stufe $ 1$ ein, und streichen von den schon vorhandenen Vektoren in Stufe $ 1$ eine geeignete Auswahl, so daß das Tableau weiterhin in Stufe $ 1$ eine Basis von $ \operatorname{Kern }C$ enthält. Wiederum muß aus Dimensionsgründen der schon vorhandene Vektor aus Stufe $ 1$ gestrichen werden. Also sieht unser Tableau letztlich wie folgt aus.

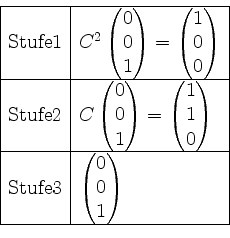
\begin{displaymath} \begin{array}{\vert l\vert l\vert}\hline \mathrm{Stufe } 1 &... ... 3 & \begin{pmatrix}0\\ 0\\ 1\end{pmatrix}\\ \hline \end{array}\end{displaymath}

Also besteht die Basis von $ \mathrm{H}_A(1)=\mathbb{C}^3$ aus einer Kette. Trägt man diese Basis als Spalten in die Matrix

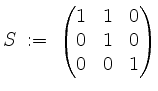
$\displaystyle S \;:=\; \begin{pmatrix}1&1&0\\ 0&1&0\\ 0&0&1\end{pmatrix}$

ein, so erhält man die Jordanform

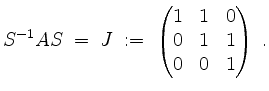
$\displaystyle S^{-1}AS \;=\; J \;:=\; \begin{pmatrix}1&1&0\\ 0&1&1\\ 0&0&1\end{pmatrix} \;. $

Anstatt $ S^{-1}AS$ tatsächlich zu berechnen, rechnen wir zur Probe

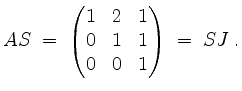
$\displaystyle AS \;=\; \begin{pmatrix}1&2&1\\ 0&1&1\\ 0&0&1\end{pmatrix} \;=\; SJ \;. $

Das Minimalpolynom ist

$\displaystyle \mu_A(X) \;=\; (X-1)^3\;, $

da die maximale Kantenlänge eines Jordanblocks zum Eigenwert $ 1$ gleich $ 3$ ist.
(Autoren: Künzer/Martin/Tentler/Wahrheit)
[Verweise]
  automatisch erstellt am 22.  8. 2006