Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Mögliche Jordanformen

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

In den folgenden Aufgaben sind Jordanformen als gleich anzusehen, falls sie bis auf Reihenfolge der Jordanblöcke übereinstimmen.

1.
Welche Jordanformen in $ \mathbb{C}^{3\times 3}$ mit Eigenwerten in $ \{ 0,1\}$ gibt es? Gib jeweils das charakteristische Polynom und das Minimalpolynom an.
2.
Welche Jordanformen mit charakteristischem Polynom $ (X^2+1)^2(X - \mathrm{i})^2$ gibt es?
3.
Welche Jordanformen mit Minimalpolynom $ X^3 - 6X^2 + 12 X - 8$ gibt es in $ \mathbb{C}^{8\times 8}$ ?

Lösung.

1.
Es gibt die folgenden Jordanformen.

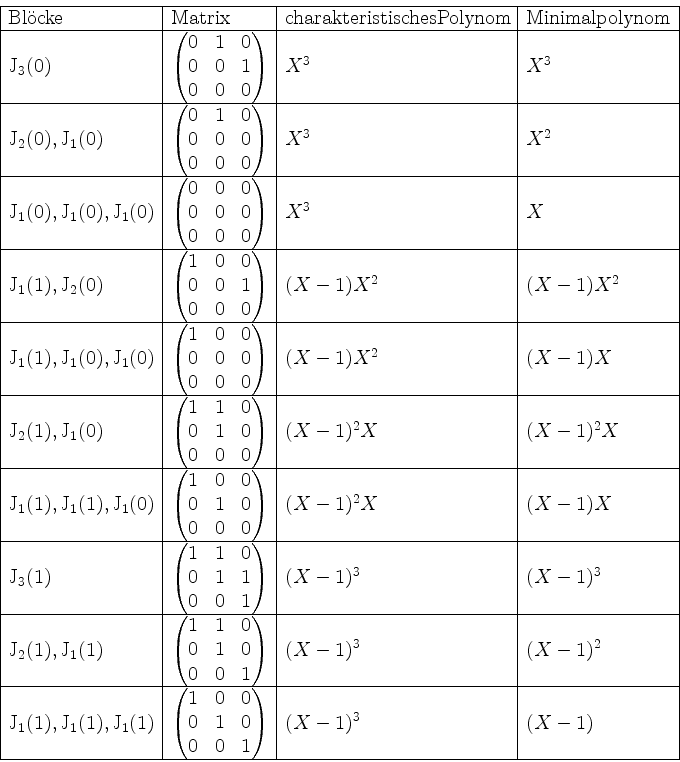
\begin{displaymath} \begin{array}{\vert l\vert l\vert l\vert l\vert}\hline \math... ...&0\\ 0&0&1\end{pmatrix} & (X-1)^3 & (X-1) \\ \hline \end{array}\end{displaymath}

2.
Es ist $ (X^2+1)^2(X - \mathrm{i})^2 = (X + \mathrm{i})^2(X - \mathrm{i})^4$ . Damit gibt es die folgenden Jordanformen.

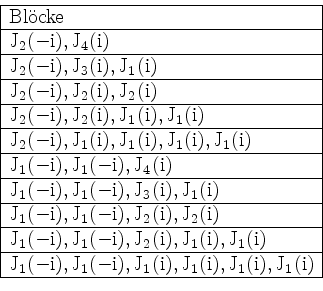
\begin{displaymath} \begin{array}{\vert l\vert}\hline \mathrm{Bl''ocke} \\ \hlin... ...J}_1(\mathrm{i}),\mathrm{J}_1(\mathrm{i}) \\ \hline \end{array}\end{displaymath}

3.
Es ist $ X^3 - 6X^2 + 12 X - 8 = (X - 2)^3$ . Damit gibt es die folgenden Jordanformen.

\begin{displaymath} \begin{array}{\vert l\vert}\hline \mathrm{J}_3(2),\mathrm{J}... ...m{J}_1(2),\mathrm{J}_1(2),\mathrm{J}_1(2) \\ \hline \end{array}\end{displaymath}

Wir bemerken noch, daß diese Matrizen bei verschiedener Jordanform alle dasselbe charakteristische Polynom und dasselbe Minimalpolynom haben.

(Autoren: Künzer/Martin/Tentler/Wahrheit)

siehe auch:

  automatisch erstellt am 11.  8. 2006