Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Spezielle Kriterien für Diagonalisierbarkeit

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Sei $ n\geq 1$ und $ A\in\mathbb{C}^{n\times n}$ . Zeige folgende Aussagen.

1.
Es gibt ein $ m\geq 1$ mit $ A^m=0$ genau dann, wenn 0 einziger Eigenwert von $ A$ ist.
2.
Die Matrix $ A$ ist diagonalisierbar genau dann, wenn $ \mu_A(X)$ nur einfache Nullstellen besitzt, d.h. wenn $ \mu_A(X)=(X-\lambda_1)\cdots(X-\lambda_r)$ mit paarweise verschiedenen $ \lambda_1,\dots,\lambda_r\in\mathbb{C}$ .
3.
Es ist $ \chi_A(X)=\mu_A(X)$ genau dann, wenn die geometrische Vielfachheit aller Eigenwerte gleich $ 1$ ist.
4.
Ist $ A^m=\mathrm{E}$ für ein $ m\geq 1$ , so ist $ A$ diagonalisierbar.
5.
Ist $ A^2=2A-\mathrm{E}$ , so ist $ A=\mathrm{E}$ oder $ A$ ist nicht diagonalisierbar. Gib ein Beispiel für den letzteren Fall an.

Lösung.

Sei $ S\in\mathbb{C}^{n\times n}$ invertierbar mit $ S^{-1}AS=J$ in Jordanform.

1.
Sei zunächst $ A^m=0$ . Es ist $ J^m=(S^{-1}AS)^m=S^{-1}A^mS=0$ und folglich $ (\mathrm{J}_k(\lambda))^m=0$ für jeden auftretenden Jordanblock $ \mathrm{J}_k(\lambda)$ . Die Hauptdiagonaleinträge von $ (\mathrm{J}_k(\lambda))^m$ sind alle gleich $ \lambda^m$ . Aus $ \lambda^m=0$ folgt nun $ \lambda=0$ . Da dies für jeden auftretenden Jordanblock gilt, ist 0 der einzige Eigenwert.

Sei nun umgekehrt 0 einziger Eigenwert von $ A$ . Dann sind alle auftretenden Jordanblöcke der Form $ \mathrm{J}_k(0)$ für gewisse $ k\geq 1$ , und es ist $ (\mathrm{J}_k(0))^k=0$ . Sei $ m$ die maximale Kantenlänge aller auftretenden Jordanblöcke. Dann ist $ J^m=0$ , und es folgt $ A^m=SJ^mS^{-1}=0$ .

Alternativ ist $ A^m=0$ für ein $ m\geq 1$ genau dann, wenn $ \mu_A(X)=X^l$ für ein $ l\geq 1$ , was wiederum genau dann gilt, wenn 0 einziger Eigenwert von $ A$ ist.

2.
Die Matrix $ A$ ist diagonalisierbar genau dann, wenn $ J$ eine Diagonalmatrix ist, was genau dann der Fall ist, wenn alle Jordanblöcke die Kantenlänge eins haben, was schließlich genau dann der Fall ist, wenn $ \mu_A(X)$ nur einfache Nullstellen hat.

3.
Sei $ \chi_A(X)=(X-\lambda_1)^{m_1}\cdots(X-\lambda_r)^{m_r}$ und $ \mu_A(X)=(X-\lambda_1)^{l_1}\cdots(X-\lambda_r)^{l_r}$ , wobei $ \lambda_1,\dots,\lambda_r$ paarweise verschieden seien. Es ist die Summe der Kantenlängen aller Jordanblöcke zum Eigenwert $ \lambda_i$ gleich $ m_i$ .

Daher ist $ \chi_A(X)=\mu_A(X)$ genau dann, wenn $ m_i=l_i$ ist für alle $ i$ , was genau dann der Fall ist, wenn für jedes $ i$ genau ein Jordanblock existiert, und zwar mit Kantenlänge $ m_i$ , was schließlich dazu äquivalent ist, daß jeder Eigenwert geometrische Vielfachheit eins besitzt.

4.
Aus $ A^m=\mathrm{E}$ folgt $ J^m = S^{-1} A^m S = \mathrm{E}$ . Träte in $ J$ ein Jordanblock $ \mathrm{J}_k(\lambda)$ mit $ k\geq 2$ auf, so wäre $ (\mathrm{J}_k(\lambda))^m = \mathrm{E}$ . Auf der ersten oberen Nebendiagonalen von $ (\mathrm{J}_k(\lambda))^m$ findet sich der Eintrag $ m\lambda^{k-1}$ , wie eine Induktion zeigt. Aus $ m\lambda^{k-1} = 0$ folgt nun $ \lambda=0$ . Nun steht aber in der Hauptdiagonalen von $ (\mathrm{J}_k(\lambda))^m$ eine Null, im Widerspruch zu $ (\mathrm{J}_k(\lambda))^m = \mathrm{E}$ . Also haben alle Jordanblöcke Kantenlänge eins, und es folgt $ A$ diagonalisierbar.

Alternativ, mit $ f(X):=X^m-1$ gilt $ f(A)=0$ . Daher ist $ \mu_A(X)$ ein Teiler von $ X^m-1$ . Die Nullstellen von $ f(X)$ sind genau die $ m$ -ten Einheitswurzeln $ \zeta_m^k:=\exp(2\pi\mathrm{i} k/m)$ für $ k\in\{0,\dots,m-1\}$ , und diese sind paarweise verschieden. Es folgt $ X^m-1=(X-\zeta_m^0)\cdots(X-\zeta_m^{m-1})$ . Also besitzt $ f(X)$ und somit auch $ \mu_A(X)$ nur einfache Nullstellen, und folglich ist $ A$ diagonalisierbar.

5.
Mit $ f(X):=X^2-2X+1=(X-1)^2$ ist $ f(A)=0$ . Somit ist $ \mu_A(X)=X-1$ oder $ \mu_A(X)=(X-1)^2$ . Im Falle $ \mu_A(X)=X-1$ ist wegen $ \mu_A(A)=0$ mithin $ A=\mathrm{E}$ . Im Falle $ \mu_A(X)=(X-1)^2$ hat $ \mu_A(X)$ eine doppelte Nullstelle, und daher ist $ A$ dann nicht diagonalisierbar.

Zum Beispiel erfüllt die Matrix 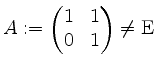$ A:=\begin{pmatrix}1&1\\ 0&1\end{pmatrix}\ne\mathrm{E}$ die Gleichung $ A^2=2A-\mathrm{E}$ .

(Autoren: Künzer/Martin/Tentler/Wahrheit)

siehe auch:

  automatisch erstellt am 11.  8. 2006