Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Unitäre Diagonalisierbarkeit

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Sei

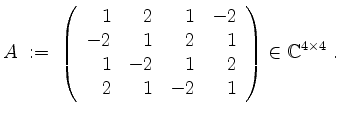
$\displaystyle A \;:=\; \left(\begin{array}{rrrr} 1 & 2 & 1 & -2 \\ -2 & 1 & 2 ... ...1 &-2 & 1 & 2 \\ 2 & 1 &-2 & 1 \end{array}\right)\in\mathbb{C}^{4\times 4}\;. $

Überprüfe $ A$ auf unitäre Diagonalisierbarkeit. Bestimme gegebenenfalls eine unitäre Matrix $ U\in\mathbb{C}^{4\times 4}$ und eine Diagonalmatrix $ D\in\mathbb{C}^{4\times 4}$ so, daß $ \bar{U}^\mathrm{t} AU=D$ .

Lösung.

Es wird

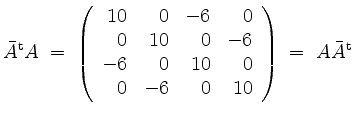
$\displaystyle \bar{A}^\mathrm{t} A \;=\; \left(\begin{array}{rrrr} 10 & 0 & -6 ... ... 0 & 10 & 0 \\ 0 & -6 & 0 & 10 \end{array}\right) \;=\; A\bar{A}^\mathrm{t}\, $

d.h. $ A$ ist normal und damit unitär diagonalisierbar.

Das charakteristische Polynom ergibt sich zu

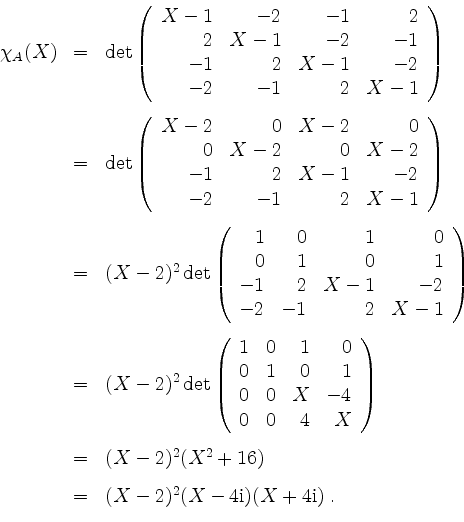
\begin{displaymath} \begin{array}{rcl} \chi_A(X) &=& \det\left(\begin{array}{rr... ...} \\ &=& (X-2)^2 (X-4\mathrm{i})(X+4\mathrm{i})\;. \end{array}\end{displaymath}

Also sind $ 2$ , $ 4\mathrm{i}$ und $ -4\mathrm{i}$ die Eigenwerte von $ A$ .

Die Eigenräume von $ A$ ergeben sich wie folgt.

Es wird

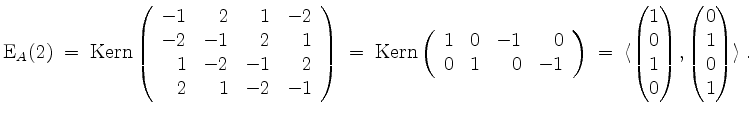
$\displaystyle \mathrm{E}_A(2) \;=\; \operatorname{Kern}\left(\begin{array}{rrrr... ...1\\ 0\\ 1\\ 0\end{pmatrix},\begin{pmatrix}0\\ 1\\ 0\\ 1\end{pmatrix}\rangle\;. $

Eine Orthonormalbasis von $ \mathrm{E}_A(2)$ ergibt sich zu

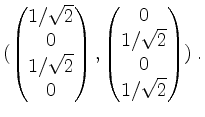
$\displaystyle (\begin{pmatrix}1/\sqrt{2}\\ 0\\ 1/\sqrt{2}\\ 0\end{pmatrix},\begin{pmatrix}0\\ 1/\sqrt{2}\\ 0\\ 1/\sqrt{2}\end{pmatrix})\;. $

Es wird

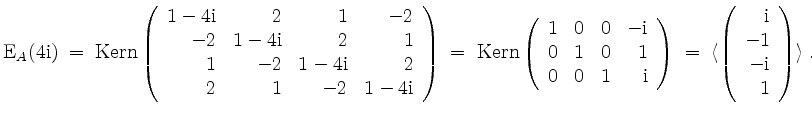
$\displaystyle \mathrm{E}_A(4\mathrm{i}) \;=\; \operatorname{Kern}\left(\begin{a... ...(\begin{array}{r}\mathrm{i}\\ -1\\ -\mathrm{i}\\ 1\end{array}\right)\rangle\;. $

Eine Orthonormalbasis von $ \mathrm{E}_A(4\mathrm{i})$ ergibt sich zu

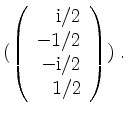
$\displaystyle (\left(\begin{array}{r}\mathrm{i}/2\\ -1/2\\ -\mathrm{i}/2\\ 1/2\end{array}\right))\;. $

Es wird

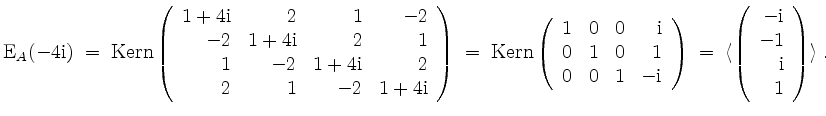
$\displaystyle \mathrm{E}_A(-4\mathrm{i}) \;=\; \operatorname{Kern}\left(\begin{... ...(\begin{array}{r}-\mathrm{i}\\ -1\\ \mathrm{i}\\ 1\end{array}\right)\rangle\;. $

Eine Orthonormalbasis von $ \mathrm{E}_A(-4\mathrm{i})$ ergibt sich zu

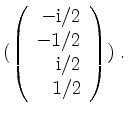
$\displaystyle (\left(\begin{array}{r}-\mathrm{i}/2\\ -1/2\\ \mathrm{i}/2\\ 1/2\end{array}\right))\;. $

Zur Probe verifizieren wir, daß die Eigenräume bezüglich verschiedener Eigenräume in der Tat zueinander orthogonal sind.

Zusammengesetzt erhalten wir also mit

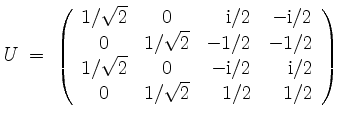
$\displaystyle U \;=\; \left(\begin{array}{ccrr} 1/\sqrt{2} & 0 & \mathrm{i}/2 &... ...thrm{i}/2 & \mathrm{i}/2 \\ 0 & 1/\sqrt{2} & 1/2 & 1/2 \\ \end{array}\right) $

die unitäre Diagonalisierung

$\displaystyle \bar{U}^\mathrm{t} A U \;=\; \mathrm{diag}(2,2,4\mathrm{i},-4\mathrm{i})\; . $

(Autoren: Künzer/Martin/Tentler/Wahrheit)

siehe auch:

  automatisch erstellt am 22.  8. 2006