Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Kompaktheit

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht
Untersuche folgende Mengen auf Kompaktheit.
1.
$ K=\{(x,y)^\mathrm{t}\in\mathbb{R}^2\,\vert\, 1\leq x^2+y^2\leq 4,\; x\geq 0\}$ .
2.
$ K=\{(x,\sin\frac{1}{x})^\mathrm{t}\in\mathbb{R}^2\,\vert\, x\in(0,1]\} $ .
3.
$ K=\{(\cos x,\sin x,x)^\mathrm{t}\in\mathbb{R}^3\,\vert\, x\geq 0\}$ .
4.
$ K=\{x\}\cup\{x_k\vert\;k\ge 1\}$ , wobei $ (x_k)_{k\ge 1}$ eine konvergente Folge im $ \mathbb{R}^n$ sei, die gegen $ x$ konvergiere.

Lösung.

1.
Für alle $ (x,y)^\mathrm{t}\in K$ gilt

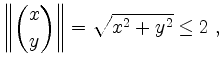
$\displaystyle \left\Vert{x\choose y}\right\Vert=\sqrt{x^2+y^2}\leq 2\;, $

d.h. die Menge $ K$ ist beschränkt.

Sei ferner $ (a_k)_{k\ge 1}=((x_k,y_k)^\mathrm{t})_{k\ge 1}$ eine konvergente Folge mit $ a_k\in K$ für alle $ k\ge 1$ und $ a:=(x_0,y_0)^\mathrm{t}:=\lim\limits_{k\to\infty} a_k$ . Dann gilt $ x_k\to x_0$ und $ y_k\to y_0$ für $ k\to\infty$ , und

$\displaystyle 1\leq x_k^2+y_k^2\leq 4,\; x_k\geq 0 $

für alle $ k\ge 1$ . Mit $ k\to\infty$ folgt daraus

$\displaystyle 1\leq x_0^2+y_0^2\leq 4,\; x_0\geq 0\;, $

d.h. $ a=(x_0,y_0)^\mathrm{t}\in K$ .

Dies bedeutet, daß die Menge $ K$ alle ihre Berührpunkte enthält, d.h. sie ist abgeschlossen.

Da $ K$ beschränkt und abgeschlossen ist, ist sie kompakt.

2.
Wir zeigen, daß die Menge $ K$ nicht abgeschlossen ist.

Die Folge $ (a_k)_{k\ge 1}$ , definiert durch

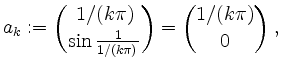
$\displaystyle a_k:={1/(k\pi)\choose\sin\frac{1}{1/(k\pi)}}={1/(k\pi)\choose 0}\;, $

liegt in der Menge $ K$ und konvergiert gegen den Punkt $ (0,0)^\mathrm{t}$ für $ k\to\infty$ . Dieser Punkt gehört jedoch nicht zur Menge $ K$ , so daß $ K$ nicht abgeschlossen ist.

Da die Menge $ K$ nicht abgeschlossen ist, kann sie insbesondere nicht kompakt sein.

3.
Wir zeigen, daß die Menge $ K$ nicht beschränkt ist.

Es ist

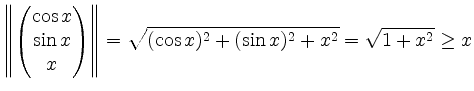
$\displaystyle \left\Vert \begin{pmatrix} \cos x\\ \sin x\\ x \end{pmatrix}\right\Vert = \sqrt{(\cos x)^2 + (\sin x)^2 + x^2} = \sqrt{1 + x^2} \geq x $

für alle $ x \geq 0$ . Demzufolge ist die Menge $ K$ nicht beschränkt und daher auch nicht kompakt.

4.
Wir wollen den Satz von Heine-Borel verwenden. Es sei also $ (U_i)_{i\in I}$ eine offene Überdeckung der Menge $ K$ . Dann gibt es ein $ j\in I$ so, daß $ x\in U_j$ . Da $ U_j$ offen ist, gibt es ein $ \varepsilon>0$ so, daß

$\displaystyle B_{\varepsilon}(x) \;\subseteq\; U_j\;. $

Wegen $ x_k\to x$ gibt es ein $ N\ge 1$ so, daß für alle $ k\ge N$ gilt

$\displaystyle \Vert x_k-x\Vert \;<\; \varepsilon\;. $

Daher liegen die Punkte $ x_N,x_{N+1},\ldots$ alle in $ U_j$ . Zu jedem $ k\in\{1,\ldots,N-1\}$ gibt es zudem ein $ i_k\in I$ so, daß $ x_k\in U_{i_k}$ . Also gilt

$\displaystyle K \;\subseteq\; U_{i_1}\cup U_{i_2}\cup\ldots\cup U_{i_{N-1}} \cup U_j\;. $

Also besitzt die offene Überdeckung $ (U_i)_{i\in I}$ die Teilüberdeckung $ (U_i)_{i\in I_0}$ mit $ I_0:=\{i_1,\ldots,i_{N-1},j\}$ .

Nach dem Satz von Heine-Borel ist die Menge $ K$ demnach kompakt.

(Autoren: Künzer/Martin/Tentler/Wahrheit)
[Verweise]
  automatisch erstellt am 11.  8. 2006