
Mathematik-Online-Lexikon:

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online-Lexikon: | |
Richtungsableitungen und Differenzierbarkeit |
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z | Übersicht |
Es sei
![]() gegeben durch
gegeben durch
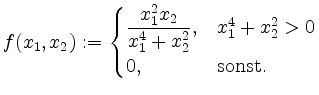
Zeige, daß die Richtungsableitung von ![]() in allen
in allen
![]() in jede Richtung
in jede Richtung
![]() existiert, die Funktion
existiert, die Funktion ![]() jedoch nicht differenzierbar
ist.
jedoch nicht differenzierbar
ist.
Lösung.
Die gegebene Funktion ![]() ist als Komposition differenzierbarer Funktionen
differenzierbar in allen Punkten
ist als Komposition differenzierbarer Funktionen
differenzierbar in allen Punkten
![]() mit
mit
![]() . Damit existieren insbesondere auch alle
Richtungsableitungen von
. Damit existieren insbesondere auch alle
Richtungsableitungen von ![]() in diesen Punkten.
in diesen Punkten.
Wir untersuchen nun die Existenz der Richtungsableitung von ![]() in dem Punkt
in dem Punkt
![]() in Richtung
in Richtung
![]() .
Dabei unterscheiden wir zwei Fälle.
.
Dabei unterscheiden wir zwei Fälle.
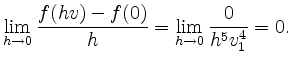
Folglich ist
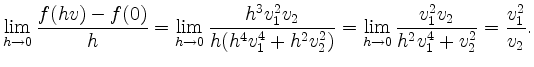
Wir zeigen nun, daß die Funktion ![]() nicht differenzierbar ist, indem wir zeigen, daß sie nicht
stetig im Punkt
nicht differenzierbar ist, indem wir zeigen, daß sie nicht
stetig im Punkt
![]() ist.
ist.
Für die Folge
![]() mit
mit
![]() ist nämlich
ist nämlich
![]() für
für
![]() , wohingegen
, wohingegen
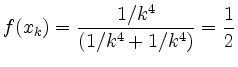
für alle
Skizze von ![]() .
.
![\includegraphics[width = 8cm]{l2.eps}](/inhalt/beispiel/beispiel1127/img25.png)
siehe auch:
| automatisch erstellt am 11. 8. 2006 |