Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Ableitungen und Hessematrix

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Berechne die Ableitungen der folgenden Funktionen $ f$ , sowie die Hessematrix, sofern diese definiert ist.

1.
$ f:\mathbb{R}^n\setminus\{ 0 \} \to \mathbb{R}, x \mapsto \Vert x \Vert$
2.
$ f:\mathbb{R}^n \to \mathbb{R}^m, x \mapsto Ax+b$ , mit $ A \in \mathbb{R}^{m \times n}, b \in \mathbb{R}^m$
3.
$ f:\mathbb{R}^n \to \mathbb{R}, x \mapsto x^\mathrm{t} A x$ , mit einer symmetrischen Matrix $ A \in \mathbb{R}^{n \times n}$

Lösung.

1.
Die Funktion $ f$ ist differenzierbar als Komposition differenzierbarer Funktionen. Mit $ x=(x_1, \ldots, x_n)^\mathrm{t} \in \mathbb{R}^n$ ist $ \Vert x \Vert = \sqrt{x_1^2 + \cdots + x_n^2}$ , und damit erhalten wir die partiellen Ableitungen

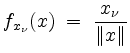
$\displaystyle f_{x_\nu}(x) \;=\; \frac{x_\nu}{\Vert x \Vert} $

für $ \nu\in\{1,\dots,n\}$ . Es ergibt sich für $ x \ne 0$

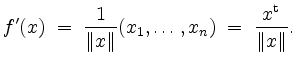
$\displaystyle f'(x) \;=\; \frac{1}{\Vert x \Vert} (x_1, \ldots, x_n) \;=\; \frac{x^\mathrm{t}}{\Vert x \Vert}. $

Eine alternative Berechnung ergibt sich aus den Ableitungsregeln zu

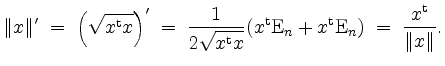
$\displaystyle \Vert x \Vert' \;=\; \left(\sqrt{x^\mathrm{t} x}\right)' \;=\; \f... ...rm{E}_n + x^\mathrm{t} \mathrm{E}_n) \;=\; \frac{x^\mathrm{t}}{\Vert x \Vert}. $

Die Hessematrix läßt sich mit den Methoden der eindimensionalen Analysis bestimmen zu

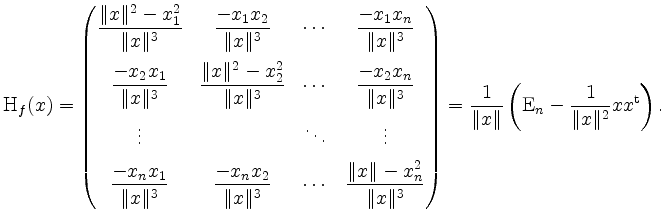
$\displaystyle \mathrm{H}_f(x) = \begin{pmatrix} \dfrac{ \Vert x \Vert^2 - x_1^... ...\Vert} \left( \mathrm{E}_n - \frac{1}{\Vert x \Vert^2} x x^\mathrm{t} \right). $

Alternativ kann man mit der Produkt- und Kettenregel wie folgt argumentieren.

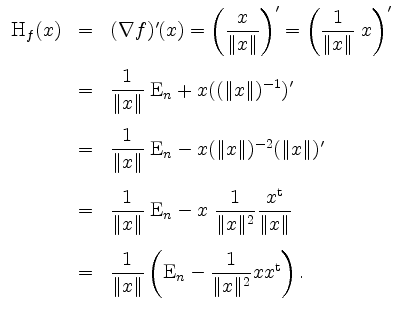
$\displaystyle \begin{array}{rcl} \mathrm{H}_f(x) & = & (\nabla f)'(x) = \left(\... ...( \mathrm{E}_n - \dfrac{1}{\Vert x \Vert^2} x x^\mathrm{t} \right). \end{array}$

2.
Die Funktion $ f$ ist differenzierbar als Komposition differenzierbarer Funktionen. Es seien $ A=(a_{i,j})_{i \in \{ 1, \ldots, m \}, j \in \{ 1, \ldots, n \}}$ , $ x=(x_1, \ldots, x_n)^\mathrm{t}$ und $ b = (b_1, \ldots, b_m)^\mathrm{t}$ . Dann ist

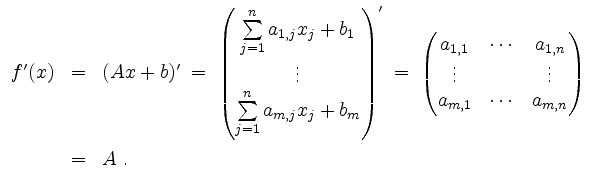
$\displaystyle \begin{array}{rcl} f'(x) &=& (Ax+b)' \;=\; \begin{pmatrix} \sum\l... ... a_{m,1} & \cdots & a_{m,n} \end{pmatrix}\vspace*{2mm}\\ &=& A\;. \end{array}$

Die Hessematrix ist nur für Funktionen erklärt, die in die reellen Zahlen $ \mathbb{R}$ abbilden. Folglich existiert die Hessematrix von $ f$ nur im Fall $ m=1$ .

In diesem Fall sind die ersten partiellen Ableitungen konstant und folglich ergibt sich die Hessematrix von $ f$ zu $ \mathrm{H}_f(x)=0\in\mathbb{R}^{n\times n}$ .

3.
Die Funktion $ f$ ist differenzierbar als Komposition differenzierbarer Funktionen, und wir erhalten mittels der Rechenregeln für totale Ableitungen unter Verwendung des Aufgabenteils 2 und der Symmetrie der Matrix $ A$

$\displaystyle (x^\mathrm{t} A x)' \; =\; (A x)^\mathrm{t} x' + x^\mathrm{t} (A ... ...; x^\mathrm{t} A \, \mathrm{E}_n + x^\mathrm{t} A \; =\; 2 x^\mathrm{t} A \; . $

Es gilt also $ (\nabla f)(x)=2Ax$ . Mit Hilfe von 2. ergibt sich

$\displaystyle \mathrm{H}_f(x) \;=\; (\nabla f)'(x) \;=\; (2 A x)' \;=\; 2 A\;. $

(Autoren: Künzer/Martin/Tentler/Wahrheit)

siehe auch:

  automatisch erstellt am 11.  8. 2006