Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Extrema und Sattelpunkte

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Bestimme alle lokalen Extrema und Sattelpunkte der auf ganz $ \mathbb{R}^2$ definierten Funktion $ f(x,y) := (x^3 - 12 x)e^{y^3 - 3y}$ .

Lösung.

Es wird

$\displaystyle f'(x,y) \; = \; e^{y^3-3y}\; \begin{pmatrix} (3 x^2 - 12) \; , & (x^3 -12 x) (3 y^2 - 3) \end{pmatrix}$

und

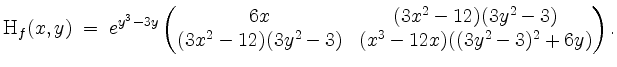
$\displaystyle \mathrm{H}_f(x,y) \; = \; e^{y^3 - 3 y} \begin{pmatrix} 6x & (3 x... ...\ (3 x^2 - 12) (3 y^2 -3) & (x^3 - 12 x) ( (3 y^2 -3)^2 + 6y ) \end{pmatrix}. $

Die notwendige Bedingung für lokale Extrema $ \nabla f(x,y)=0$ liefert die zu erfüllenden Gleichungen

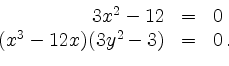
\begin{displaymath} \begin{array}{rcl} 3x^2 - 12 & = & 0 \\ (x^3 -12 x) (3 y^2 - 3) & = & 0\,. \\ \end{array}\end{displaymath}

Aus der ersten Gleichung erhalten wir $ x = \pm 2$ , und folglich aus der zweiten $ y = \pm 1$ . Die kritischen Punkte sind somit gegeben durch

$\displaystyle (-2,-1)^\mathrm{t}\; , \;\; (-2,1)^\mathrm{t}\; , \;\; (2,-1)^\mathrm{t}\; , \;\; (2,1)^\mathrm{t}\; . $

Es ist

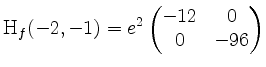
$\displaystyle \mathrm{H}_f(-2,-1) = e^{2} \begin{pmatrix} -12 & 0\\ 0 & -96 \end{pmatrix}$

negativ definit, und somit besitzt $ f$ ein lokales Maximum in $ (-2,-1)^\mathrm{t}$ .

Es ist

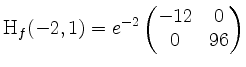
$\displaystyle \mathrm{H}_f(-2,1) = e^{-2} \begin{pmatrix} -12 & 0\\ 0 & 96 \end{pmatrix}$

indefinit, und folglich besitzt $ f$ einen Sattelpunkt in $ (-2,1)^\mathrm{t}$ .

Es ist

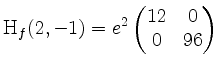
$\displaystyle \mathrm{H}_f(2,-1) = e^{2} \begin{pmatrix} 12 & 0\\ 0 & 96 \end{pmatrix}$

positiv definit, und folglich besitzt $ f$ ein lokales Minimum in $ (2,-1)^\mathrm{t}$ .

Es ist

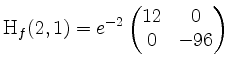
$\displaystyle \mathrm{H}_f(2,1) = e^{-2} \begin{pmatrix} 12 & 0\\ 0 & -96 \end{pmatrix}$

indefinit, und folglich besitzt $ f$ einen Sattelpunkt in $ (2,1)^\mathrm{t}$ .

Skizze von $ f$ .

\includegraphics[width = 8cm]{l1.eps}
(Autoren: Künzer/Martin/Tentler/Wahrheit)
[Verweise]
  automatisch erstellt am 11.  8. 2006