Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Implizite Funktionen

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Es sei $ f:\mathbb{R}^2\to\mathbb{R}$ definiert durch $ f(x,y):=2xy+y^3+e^{x-y-1}-1$ . Zeige, daß die Gleichung $ f(x,y)=0$ um den Punkt $ (1,0)^\mathrm{t}$ lokal eindeutig nach $ y$ auflösbar ist. Sei $ g$ die dadurch implizit definierte Funktion. Berechne $ g'(1)$ .

Lösung.

Es wird

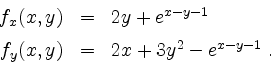
\begin{displaymath} \begin{array}{rcl} f_x(x,y) &=& 2y+e^{x-y-1} \vspace*{2mm}\\ f_y(x,y) &=& 2x+3y^2-e^{x-y-1}\;. \end{array}\end{displaymath}

Also ist $ f$ stetig differenzierbar, $ f(1,0)=0$ und $ \det f_y(1,0)=1\ne 0$ . Nach dem Satz über implizite Funktionen ist die Gleichung $ f(x,y)=0$ um den Punkt $ (1,0)$ lokal eindeutig nach $ y$ auflösbar. Also gibt es Umgebungen $ U_0\subseteq\mathbb{R}$ von $ 1$ und $ V_0\subseteq\mathbb{R}$ von 0 sowie genau eine (implizit definierte) stetig differenzierbare Funktion $ g:U_0\to V_0$ so, daß

Als Ableitung von $ g$ in $ 1$ ergibt sich

$\displaystyle g'(1) \;=\; -f_y(1,0)^{-1} f_x(1,0) \;=\; -1 \; . $

Über die Größe von $ U_0$ und $ V_0$ können wir keine Aussage machen. Jedenfalls können wir nicht beide beliebig groß wählen, wie untenstehende Skizze, in der die Lösungsmenge der Gleichung $ f(x,y)=0$ dargestellt wird, zeigt. In anderen Worten, eine globale Auflösung der Gleichung $ f(x,y)=0$ ist nicht möglich.

\includegraphics[width = 8cm]{l1.eps}
(Autoren: Künzer/Martin/Tentler/Wahrheit)

siehe auch:

  automatisch erstellt am 11.  8. 2006