Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Kurvenintegrale und konservative Vektorfelder

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Berechne jeweils das Kurvenintegral von $ f$ längs $ \gamma$ . Ist das Vektorfeld $ f$ konservativ? Berechne gegebenenfalls eine Stammfunktion von $ f$ .

  1. $ f:\mathbb{R}^2\to\mathbb{R}^2$ , $ f(x,y)=(y,y-x)^\mathrm{t}$ , $ \gamma:[0,2]\to\mathbb{R}^2$ , $ \gamma(t)=(t,t^2)^\mathrm{t}$ .
  2. $ f:\mathbb{R}^3\to\mathbb{R}^3$ , $ f(x,y,z)=(3x^2y^2z+1,\; 2x^3yz+z,\; x^3y^2+y)^\mathrm{t}$ , $ \gamma:[0,\pi]\to\mathbb{R}^3$ , $ \gamma(t) = (e^t,\; \cos t,\; t^2+1)^\mathrm{t}$ .

Lösung.

  1. Zunächst berechnen wir

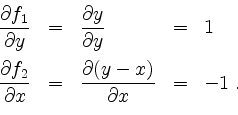
    \begin{displaymath} \begin{array}{rclcl} \dfrac{\partial f_1}{\partial y} &=& \d... ... x} &=& \dfrac{\partial(y-x)}{\partial x} &=& -1\;. \end{array}\end{displaymath}

    Also erfüllt $ f$ nicht die Integrabilitätsbedingungen und besitzt daher auch keine Stammfunktion.

    Das Kurvenintegral von $ f$ längs $ \gamma$ ergibt sich zu

    \begin{displaymath} \begin{array}{rcl} \displaystyle\int_\gamma f &=& \displayst... ...{3}\right]_0^2\vspace*{2mm}\\ &=& \dfrac{16}{3}\;. \end{array}\end{displaymath}

  2. Hier erfüllt $ f$ die Integrabilitätsbedingungen, denn es gilt

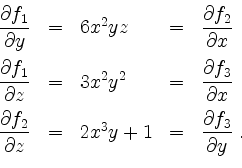
    \begin{displaymath} \begin{array}{rclcl} \dfrac{\partial f_1}{\partial y} &=& 6x... ...&=& 2x^3y+1 &=& \dfrac{\partial f_3}{\partial y}\;. \end{array}\end{displaymath}

    Ferner ist der Definitionsbereich von $ f$ ein sternförmiges, also einfach zusammenhängendes Gebiet, nämlich $ \mathbb{R}^2$ . Nach dem zweiten Hauptsatz für Kurvenintegrale ist das Vektorfeld $ f$ also konservativ.

    Wir wollen nun eine Stammfunktion $ F$ von $ f$ berechnen. Hierzu iteriert man ,,partielles Aufleiten``.

    Zunächst wird

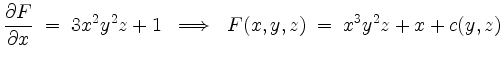
    $\displaystyle \dfrac{\partial F}{\partial x} \;=\; 3x^2y^2z+1 \;\implies\; F(x,y,z) \;=\; x^3y^2z+x+c(y,z) $

    mit einer stetig differenzierbaren Funktion $ c = c(y,z)$ , die nicht von $ x$ abhängt.

    Weiter gilt

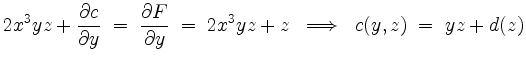
    $\displaystyle 2x^3yz+\dfrac{\partial c}{\partial y} \;=\; \dfrac{\partial F}{\partial y} \;=\; 2x^3yz+z \;\implies\; c(y,z) \;=\; y z + d(z) $

    für eine stetig differenzierbare Funktion $ d = d(z)$ , die weder von $ x$ noch von $ y$ abhängt.

    Schließlich gilt

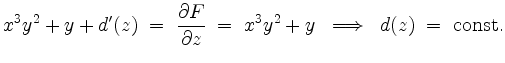
    $\displaystyle x^3y^2+y+d'(z) \;=\; \dfrac{\partial F}{\partial z} \;=\; x^3 y^2 + y \;\implies\; d(z) \;=\; \mathrm{const.} $

    Wir können also $ d(z)=0$ wählen und erhalten als eine Stammfunktion

    $\displaystyle F(x,y,z) \;=\; x^3y^2z+x+yz\; . $

    Diese ist nur bis auf eine additive Konstante bestimmt.

    Nach dem ersten Hauptsatz für Kurvenintegrale wird nun

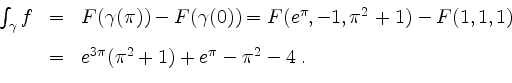
    \begin{displaymath} \begin{array}{rcl} \int_\gamma f &=& F(\gamma(\pi))-F(\gamma... ...pace{3mm}\\ &=& e^{3\pi}(\pi^2+1)+e^\pi-\pi^2-4\;. \end{array}\end{displaymath}

(Autoren: Künzer/Martin/Tentler/Wahrheit)
[Verweise]
  automatisch erstellt am 11.  8. 2006