Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Kurvenintegrale

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Sei $ F(x,y) := (x^2 + y^2)^{-1/2} + x$ eine Funktion auf $ \mathbb{R}^3\setminus\{ 0\}$ , und sei $ f = \nabla F$ das zugehörige konservative Vektorfeld.

Berechne jeweils $ \int_\gamma f$ direkt. Die Stammfunktion liefert natürlich in beiden Fällen den Wert $ F(0,1) - F(1,0) = -1$ .

1.
$ \gamma(t) := (1,t)^\mathrm{t}$ für $ t\in [0,1]$ und $ \gamma(t) := (2-t,1)^\mathrm{t}$ für $ t\in [1,2]$ .
2.
$ \gamma(t) := (\cos t,\sin t)$ für $ t\in [0,\pi/2]$ .

Lösung.

Es ist $ f(x,y) = \left(x(x^2 + y^2)^{-1/2} + 1, y(x^2 + y^2)^{-1/2}\right)^\mathrm{t}$ .

1.
Es wird

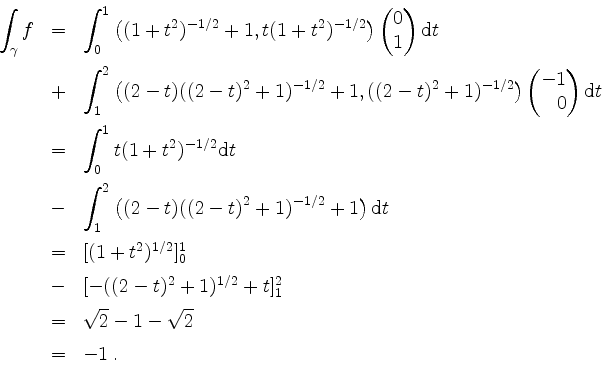
\begin{displaymath} \begin{array}{rcl} \displaystyle\int_\gamma f & = & \displa... ...} - 1 - \sqrt{2} \vspace*{2mm} \\ & = & -1\; . \\ \end{array}\end{displaymath}

2.
Es wird

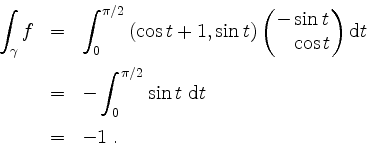
\begin{displaymath} \begin{array}{rcl} \displaystyle\int_\gamma f & = & \display... ...\sin t\ \mathrm{d}t \vspace*{2mm} \\ & = & -1 \; . \end{array}\end{displaymath}

Man hätte in 1. die Tatsache, daß sich die Integrale über die Teilwege im wesentlichen wegheben, durch ungeschicktere Wegwahl auf Kosten der Lösungsdauer noch besser verschleiern können. Aber die Aussage sollte auch so klar sein: eine geschickte Wegwahl kann bei der Berechnung eines Wegintegrales in einem konservativen Vektorfeld helfen (sofern man nicht ohnehin in der Lage ist, eine Stammfunktion für dieses Vektorfeld anzugeben).

(Autoren: Künzer/Martin/Tentler/Wahrheit)
[Verweise]
  automatisch erstellt am 11.  8. 2006