Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Volumen von Rotationskörpern

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht
Es sei $ f:[a,b]\to\mathbb{R}$ eine stetige Funktion, wobei $ a,b\in\mathbb{R}$ mit $ a<b$ .
  1. Es gelte $ f(x)\geq 0$ für alle $ x\in[a,b]$ . Bestimme das Volumen des Rotationskörpers, der entsteht, wenn die vom Graphen von $ f$ und der $ x$ -Achse eingeschlossene Fläche um die $ x$ -Achse rotiert.
  2. Die Funktion $ f$ sei streng monoton, stetig differenzierbar, und es gelte $ a\geq 0$ . Bestimme das Volumen des Rotationskörpers, der entsteht, wenn die vom Graphen von $ f$ und der $ y$ -Achse eingeschlossene Fläche um die $ y$ -Achse rotiert.

  3. Bestimme das Volumen eines Kegels mit kreisförmiger Grundfläche vom Radius $ r$ und Höhe $ h$ mit Hilfe von 1.

  4. Bestimme das Volumen einer Kugel mit Radius $ r$ mit Hilfe von 1.

  5. Die Kettenlinie $ f(x)=\cosh x=\frac{e^x+e^{-x}}{2}$ , $ x\in[-1,1]$ , rotiere um die $ x$ -Achse. Bestimme das Volumen des entstehenden Rotationskörpers.

Lösung.

  1. Es sei

    $\displaystyle R \;=\; \{(x,y,z)^\mathrm{t}\in\mathbb{R}^3\;\vert\; a\leq x\leq b,\; y^2+z^2\leq (f(x))^2\} \;. $

    der Rotationskörper. Für $ x\in[a,b]$ ist der $ x$ -Schnitt von $ R$ gegeben durch

    $\displaystyle R_x \;=\; \{(y,z)^\mathrm{t}\in\mathbb{R}^2\;\vert\; y^2+z^2\leq (f(x))^2\}\;, $

    d.h. $ R_x$ ist ein Kreis mit Radius $ f(x)$ . Es folgt $ \mathrm{vol}(R_x)=\pi (f(x))^2$ . Die Projektion von $ R$ auf die $ x$ -Achse ist das Intervall $ [a,b]$ . Nach dem Prinzip von Cavalieri ergibt sich

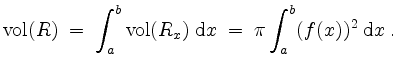
    $\displaystyle \mathrm{vol}(R) \;=\; \int_a^b\mathrm{vol}(R_x)\;\mathrm{d}x \;=\; \pi\int_a^b (f(x))^2\;\mathrm{d}x\;. $

    Alternativ kann der Inhalt auch mit der ersten Guldinschen Regel berechnet werden.

    Es sei dazu

    $\displaystyle M \;=\; \{(x,y)^\mathrm{t}\in\mathbb{R}^2\vert\; a\leq x\leq b,\; 0\leq y\leq f(x)\}\;. $

    die vom Graphen von $ f$ und der $ x$ -Achse eingeschlossene Menge. Die zweite Koordinate des Schwerpunkts $ (s_1,s_2)^\mathrm{t}$ von $ M$ ergibt sich nach Fubini zu

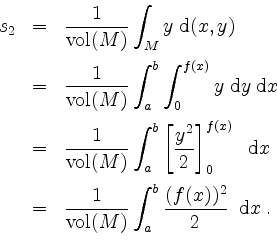
    \begin{displaymath} \begin{array}{rcl} s_2 &=& \dfrac{1}{\mathrm{vol}(M)}\displa... ...ystyle\int_a^b\dfrac{(f(x))^2}{2}\;\;\mathrm{d}x\;. \end{array}\end{displaymath}

    Nach der ersten Guldinschen Regel ist der Inhalt des Rotationskörpers $ R$ gegeben durch

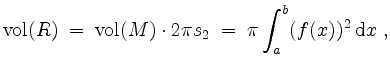
    $\displaystyle \mathrm{vol}(R) \;=\; \mathrm{vol}(M)\cdot 2\pi s_2 \;=\; \pi\int_a^b(f(x))^2\;\mathrm{d}x\;, $

    was obenstehende Rechnung nochmals bestätigt.

  2. Es sei $ I:=f([a,b])$ . Also ist $ I$ ein kompaktes Intervall, $ f:[a,b]\to I$ ist bijektiv, und $ f^{-1}:I\to[a,b]$ ist stetig.

    Es sei

    $\displaystyle R \;=\; \{(x,y,z)^\mathrm{t}\in\mathbb{R}^3\vert\; y\in I,\; x^2+z^2\leq (f^{-1}(y))^2\}\;. $

    der fragliche Rotationskörper. Für jedes $ y\in I$ ist der $ y$ -Schnitt von $ R$ gegeben durch

    $\displaystyle R^y \;=\; \{(x,z)\in\mathbb{R}^2\vert\; x^2+z^2\leq (f^{-1}(y))^2\}\;, $

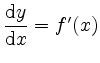    d.h. $ R^y$ ist ein Kreis mit Radius $ (f^{-1}(y))$ und Inhalt $ \pi(f^{-1}(y))^2$ . Die Projektion von $ R$ auf die $ y$ -Achse ist das Intervall $ I$ . Nach dem Prinzip von Cavalieri ergibt sich mit anschließender Substitution $ y=f(x)$ , $ \dfrac{\mathrm{d}y}{\mathrm{d}x}=f'(x)$ also

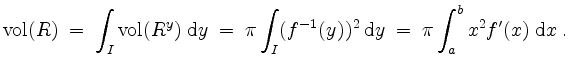
    $\displaystyle \mathrm{vol}(R) \;=\; \int_I \mathrm{vol}(R^y)\;\mathrm{d}y \;=\;... ...\int_I (f^{-1}(y))^2\;\mathrm{d}y \;=\; \pi\int_a^b x^2 f'(x)\;\mathrm{d} x\;. $

    Alternativ kann der Inhalt auch mit der ersten Guldinschen Regel berechnet werden.

    Es sei dazu

    $\displaystyle M \;=\; \{(x,y)^\mathrm{t}\in\mathbb{R}^2\vert\; y\in I,\; 0\leq x\leq f^{-1}(y)\}\;. $

    die vom Graphen von 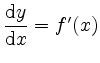$ f$ und der $ y$ -Achse eingeschlossene Menge. Die erste Koordinate des Schwerpunktes $ (s_1,s_2)^\mathrm{t}$ von $ M$ berechnet sich nach dem Satz von Fubini und anschließender Substitution $ y=f(x)$ , $ \dfrac{\mathrm{d}y}{\mathrm{d}x}=f'(x)$ zu

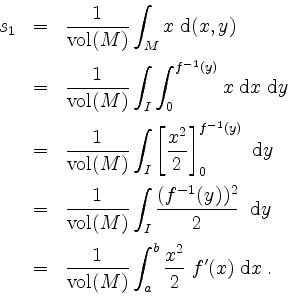
    \begin{displaymath} \begin{array}{rcl} s_1 &=& \dfrac{1}{\mathrm{vol}(M)}\displa... ...style\int_a^b\dfrac{x^2}{2}\; f'(x)\;\mathrm{d}x\;. \end{array}\end{displaymath}

    Nach der ersten Guldinschen Regel ist der Inhalt des Rotationskörpers $ R$ gegeben durch

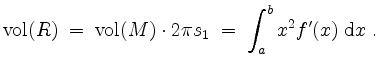
    $\displaystyle \mathrm{vol}(R) \;=\; \mathrm{vol}(M)\cdot 2\pi s_1 \;=\; \int_a^b x^2f'(x)\;\mathrm{d}x\;. $

  3. Man betrachte die Funktion

    $\displaystyle f:[0,h]\to\mathbb{R},\; f(x):=rx/h\;. $

    Dann ist der Rotationskörper, der bei Rotation des Graphen von $ f$ um die $ x$ -Achse entsteht, ein Kegel mit kreisförmiger Grundfläche vom Radius $ r$ und Höhe $ h$ . Nach 1. ist der gesuchte Inhalt gegeben durch

    $\displaystyle \pi\int_0^h(f(x))^2\;\mathrm{d}x \;=\; \pi\int_0^h \dfrac{r^2x^2}... ...;=\; \pi\left[\dfrac{r^2x^3}{3h^2}\right]_0^h \;=\; \dfrac{1}{3}\;\pi r^2 h\;, $

    in Übereinstimmung mit dem zweiten Beispiel.

  4. Man betrachte die Funktion

    $\displaystyle f:[-r,r]\to\mathbb{R}\; ,\;\;\; f(x):=\sqrt{r^2-x^2}\;. $

    Dann ist der Rotationskörper, der bei Rotation des Graphen von $ f$ um die $ x$ -Achse ensteht, eine Kugel mit Radius $ r$ . Nach 1. ist der gesuchte Inhalt gegeben durch

    $\displaystyle \pi\int_{-r}^r(f(x))^2\;\mathrm{d}x \;=\; \pi\int_{-r}^r(r^2-x^2)... ...hrm{d}x \;=\; \pi\left[r^2x-x^3/3\right]_{-r}^r \;=\; \dfrac{4}{3}\;\pi r^3\;. $

  5. Nach 1. ist der gesuchte Inhalt gegeben durch

    \begin{displaymath} \begin{array}{rcl} \pi\displaystyle\int_{-1}^1(f(x))^2\;\mat... ...right]_{-1}^1 \;=\; \pi\;\dfrac{e^2-e^{-2}+4}{4}\;. \end{array}\end{displaymath}

(Autoren: Künzer/Martin/Tentler/Wahrheit)
[Verweise]
  automatisch erstellt am 11.  8. 2006