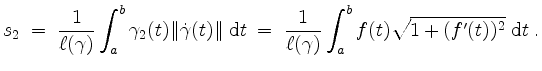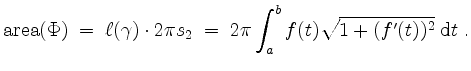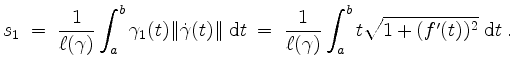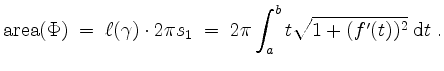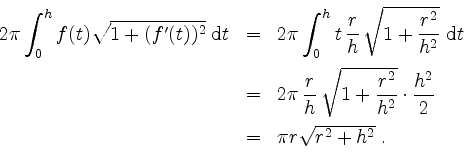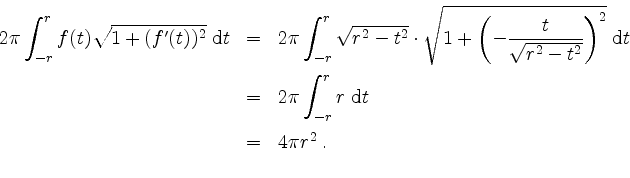Sei
![$ f:[a,b]\to\mathbb{R}$](/inhalt/beispiel/beispiel1152/img1.png) eine stetig differenzierbare Funktion, wobei
eine stetig differenzierbare Funktion, wobei
 mit
mit  .
.
- Sei
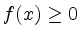 für alle
für alle ![$ x\in[a,b]$](/inhalt/beispiel/beispiel1152/img5.png) .
Gib eine Formel an für den Flächeninhalt der Rotationsfläche, die entsteht, wenn der Graph von
.
Gib eine Formel an für den Flächeninhalt der Rotationsfläche, die entsteht, wenn der Graph von  um die
um die 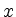 -Achse rotiert.
-Achse rotiert.
- Sei
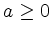 . Gib eine Formel an für den Flächeninhalt der Rotationsfläche, die entsteht,
wenn der Graph von
. Gib eine Formel an für den Flächeninhalt der Rotationsfläche, die entsteht,
wenn der Graph von  um die
um die 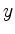 -Achse rotiert.
-Achse rotiert.
- Bestimme mit Hilfe von 1. die Mantelfläche eines Kegels mit kreisförmiger Grundfläche vom Radius
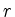 und Höhe
und Höhe 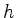 .
.
- Bestimme mit Hilfe von 1. die Oberfläche einer Kugel mit Radius
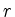 .
.
- Bestimme mit Hilfe von 1. den Flächeninhalt der Rotationsfläche, die entsteht, wenn die Kettenlinie
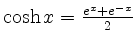 ,
,
![$ x\in[-1,1]$](/inhalt/beispiel/beispiel1152/img13.png) , um die
, um die 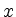 -Achse rotiert.
-Achse rotiert.
Lösung.
Sei 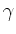 die Kurve, die den Graphen von
die Kurve, die den Graphen von  beschreibt, d.h. sei
beschreibt, d.h. sei
- Die zweite Koordinate
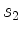 des Kurvenschwerpunkts
des Kurvenschwerpunkts
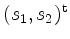 von
von 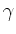 ist gegeben durch
ist gegeben durch
Also ergibt sich der gesuchte Flächeninhalt der Rotationsfläche des Graphen von  um die
um die 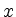 -Achse mit der zweiten Guldinschen Regel zu
-Achse mit der zweiten Guldinschen Regel zu
- Die erste Koordinate
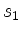 des Kurvenschwerpunkts
des Kurvenschwerpunkts
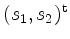 von
von 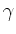 ist gegeben durch
ist gegeben durch
Also ergibt sich der gesuchte Flächeninhalt der Rotationsfläche des Graphen von  um die
um die 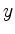 -Achse mit der zweiten Guldinschen Regel zu
-Achse mit der zweiten Guldinschen Regel zu
- Sei
![$ f:[0,h]\to\mathbb{R}$](/inhalt/beispiel/beispiel1152/img23.png) ,
,
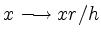 . Die zugehörige Rotationsfläche um die
. Die zugehörige Rotationsfläche um die 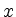 -Achse ist die gesuchte Mantelfläche und ergibt sich mit 1. zu
-Achse ist die gesuchte Mantelfläche und ergibt sich mit 1. zu
- Sei
![$ f:[-r,+r]\to\mathbb{R}$](/inhalt/beispiel/beispiel1152/img26.png) ,
,
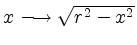 . Die zugehörige Rotationsfläche um die
. Die zugehörige Rotationsfläche um die  -Achse ist die gesuchte Kugeloberfläche und ergibt sich mit 1. zu
-Achse ist die gesuchte Kugeloberfläche und ergibt sich mit 1. zu
- Sei
![$ f:[-1,+1]\to\mathbb{R}$](/inhalt/beispiel/beispiel1152/img29.png) ,
,
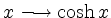 . Die zugehörige Rotationsfläche um die
. Die zugehörige Rotationsfläche um die  -Achse ergibt sich mit 1. zu
-Achse ergibt sich mit 1. zu
(Autoren: Künzer/Martin/Tentler/Wahrheit)
| |
automatisch erstellt
am 11. 8. 2006 |


![]() eine stetig differenzierbare Funktion, wobei
eine stetig differenzierbare Funktion, wobei
![]() mit
mit ![]() .
.
![]() die Kurve, die den Graphen von
die Kurve, die den Graphen von ![]() beschreibt, d.h. sei
beschreibt, d.h. sei
![$\displaystyle \gamma:[a,b]\to\mathbb{R}^2\; ,\;\;\; \gamma(t)\; :=\; {t\choose f(t)}\;.
$](/inhalt/beispiel/beispiel1152/img15.png)