Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Flächeninhalt der Astroide

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Bestimme den Flächeninhalt der Astroide, die durch die Randkurve

$\displaystyle \gamma:[0,2\pi]\to\mathbb{R}^2\;,\;\; \gamma(t)\;=\;{(\cos t)^3\choose (\sin t)^3} $

begrenzt wird, unter Verwendung des Greenschen Integralsatzes.

Skizze von $ \gamma$ .

\includegraphics[width = 8cm]{astroide.eps}

Lösung.

Nach dem Greenschen Integralsatz, angewandt auf das Vektorfeld $ f(x,y)=\frac{1}{2}(-y,x)^{\mathrm{t}}$ , ergibt sich der Inhalt der Astroide $ K$ zu

\begin{displaymath} \begin{array}{rcl} \mathrm{vol}(K) & = & \dfrac{1}{2}\;\disp... ...ht]_0^\pi\vspace*{2mm}\\ & = & \dfrac{3\pi}{8}\; . \end{array}\end{displaymath}

Alternativ kann man auch wie folgt über das Komplexe gehen, sollte man keine Sinus-Cosinus-Vereinfachung erkennen.

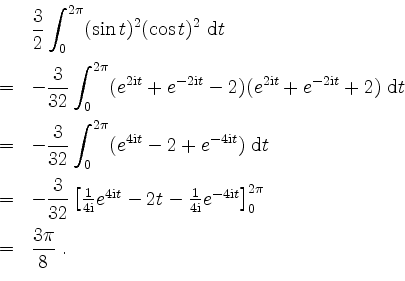
\begin{displaymath} \begin{array}{rcl} & & \dfrac{3}{2}\displaystyle\int_0^{2\pi... ...2\pi}\vspace*{2mm}\\ & = & \dfrac{3\pi}{8}\; . \\ \end{array}\end{displaymath}

Um die Plausibilität dieses Resultats zu überprüfen, beachte man, daß die Astroide in einem Quadrat der Seitenlänge $ \sqrt{2}$ enthalten ist und ihr Flächeninhalt folglich kleiner als $ 2$ sein muß.

(Autoren: Künzer/Martin/Tentler/Wahrheit)

siehe auch:

  automatisch erstellt am 11.  8. 2006