Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Stokesscher Integralsatz

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Verifiziere den Stokesschen Integralsatz für das Vektorfeld $ f:\mathbb{R}^3\to\mathbb{R}^3$ , $ f(x,y,z):=(y,z,x)^\mathrm{t}$ , und die Fläche mit dem Träger $ F=\{(x,y,z)^\mathrm{t}\in\mathbb{R}^3\;\vert\;z=x^2-y^2,\;x^2+y^2\leq 1\}$ , d.h. berechne die linke wie die rechte Seite der Gleichung des Stokesschen Integralsatzes und vergleiche die Ergebnisse.

Lösung.

Zunächst parametrisieren wir $ \;F\;$ durch

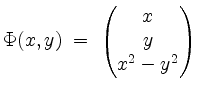
$\displaystyle \Phi(x,y)\; =\;\begin{pmatrix}x\\ y\\ x^2-y^2\end{pmatrix}$

auf $ \;K=\{(x,y)^\mathrm{t} \in \mathbb{R}^2 \;\vert\;x^2+y^2\leq 1\}\;$ . Dann ist $ \;\partial K\;$ parametrisiert durch die Kurve

$\displaystyle \gamma(t)\; =\; \begin{pmatrix}\cos t\\ \sin t\end{pmatrix}\;,\quad t\in [-\pi,\pi]\;. $

Es ist also $ \;\partial\Phi=\Phi\circ\partial K\;$ beschrieben durch

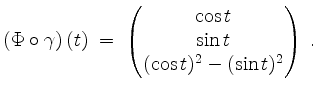
$\displaystyle \left(\Phi\circ\gamma\right)(t)\; =\;\begin{pmatrix}\cos t\\ \sin t\\ (\cos t)^2-(\sin t)^2\end{pmatrix}\; . $

Die rechte Seite der Gleichung des Stokesschen Integralsatzes ergibt sich zu

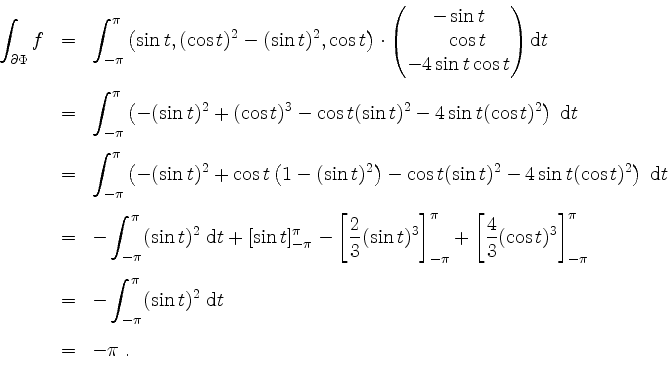
\begin{displaymath} \begin{array}{rcl} \displaystyle\int_{\partial\Phi}f &=& \di... ...i(\sin t)^2\;\mathrm{d}t\vspace{3mm}\\ &=& -\pi\;. \end{array}\end{displaymath}

Wir haben

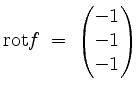
$\displaystyle \mathrm{rot }f\; =\; \begin{pmatrix}-1\\ -1\\ -1\end{pmatrix}$

sowie

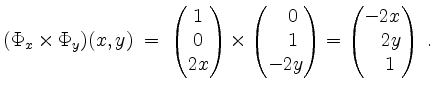
$\displaystyle (\Phi_x\times\Phi_y)(x,y)\; =\; \begin{pmatrix}1\\ 0\\ 2x\end{pma... ...y\end{pmatrix}=\begin{pmatrix}-2x\\ \hfill 2y\\ \phantom{-} 1\end{pmatrix}\; . $

Die rechte Seite der Gleichung des Stokesschen Integralsatzes ergibt sich zu

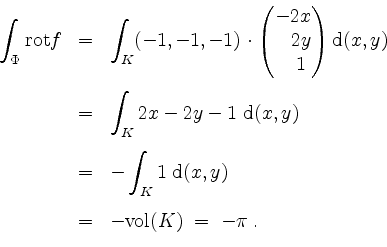
\begin{displaymath} \begin{array}{rcl} \displaystyle\int_\Phi\mathrm{rot }f &=& ... ...\ &=& \displaystyle -\mathrm{vol}(K)\; =\; -\pi\;. \end{array}\end{displaymath}

Für das drittletzte Gleichheitszeichen beachte man $ \int_K x\;\mathrm{d}(x,y)=\int_K y\;\mathrm{d}(x,y)=0$ , was sich aus einer Symmetrieüberlegung ergibt. Diese beiden Integrale berechnen nämlich gerade das $ \mathrm{vol}(K)$ -fache der Koordinaten des Schwerpunktes von $ K$ .

In der Tat stimmen also die linke und die rechte Seite der Gleichung des Stokesschen Integralsatzes im vorliegenden Fall überein.

(Autoren: Künzer/Martin/Tentler/Wahrheit)
[Verweise]
  automatisch erstellt am 11.  8. 2006