Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Gaußscher Integralsatz

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Es sei $ B$ die dreidimensionale Kugel mit Radius $ R>0$ um den Nullpunkt. Sei das Vektorfeld $ f:\mathbb{R}^3 \to \mathbb{R}^3$ definiert durch $ f(x,y,z)=(x^3,y^3,z^3)^\mathrm{t}$ .

Bestimme $ \int_{\partial B} f$ einmal durch direkte Rechnung, und einmal unter Zuhilfenahme des Satzes von Gauß.

Lösung.

Es ist

$\displaystyle \mathrm{div } f(x,y,z) \; =\; 3 (x^2+y^2+z^2)\; . $

Mit dem Gaußschen Integralsatz erhalten wir unter Verwendung von Kugelkoordinaten - bei welchen der Normalenvektor in der Tat stets nicht nach innen zeigt -

\begin{displaymath} \begin{array}{rcl} \displaystyle \int_{\partial B} f &=& \d... ...r\vspace{3mm}\\ &=& \dfrac{12}{5} \, \pi R^5 \, . \end{array}\end{displaymath}

Eine direkte Rechnung liefert, ebenfalls unter Verwendung von Kugelkoordinaten, aber etwas mühevoller,

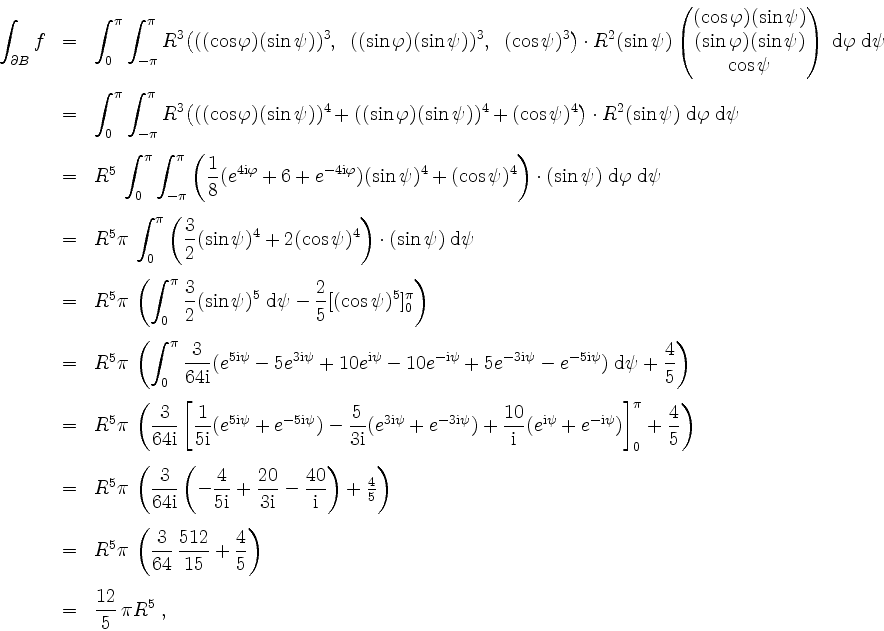
\begin{displaymath} \begin{array}{rcl} \displaystyle \int_{\partial B} f & = & ... ...space{3mm}\\ & = & \dfrac{12}{5} \, \pi R^5\; ,\\ \end{array}\end{displaymath}

wie zu erwarten.
(Autoren: Künzer/Martin/Tentler/Wahrheit)

siehe auch:

  automatisch erstellt am 11.  8. 2006