
Mathematik-Online-Lexikon:

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online-Lexikon: | |
Fourierreihe der Sägezahnfunktion |
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z | Übersicht |
Berechne die Fourierreihe der ![]() -periodischen ,,Sägezahnfunktion``, welche durch
-periodischen ,,Sägezahnfunktion``, welche durch
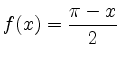 definiert ist
für
definiert ist
für
![]() . Untersuche zudem die Fourierreihe im Intervall
. Untersuche zudem die Fourierreihe im Intervall ![]() auf Konvergenz und bestimme gegebenenfalls
ihre Werte.
auf Konvergenz und bestimme gegebenenfalls
ihre Werte.
Lösung.
Reelle Berechnung der Fourierkoeffizienten.
Es ist ![]() auf
auf
![]() eine ungerade Funktion, außer bei
eine ungerade Funktion, außer bei ![]() . Also ist
. Also ist ![]() für alle
für alle ![]() .
.
Wir berechnen noch
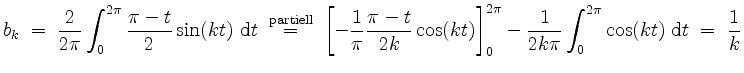
für
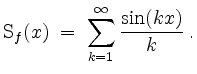
Komplexe Berechnung der Fourierkoeffizienten.
Wir erhalten für
![]() durch partielle Integration
durch partielle Integration
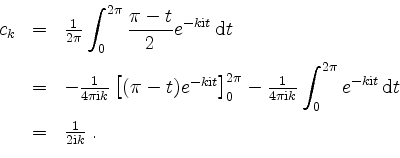
Für
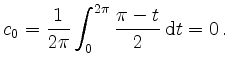
Insbesondere sind
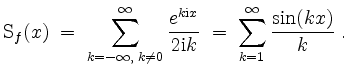
Skizze des Graphen der ersten ![]() und des Graphen der ersten
und des Graphen der ersten ![]() Summanden der Fourierreihe.
Summanden der Fourierreihe.
Da ![]() für
für
![]() differenzierbar ist, gilt dort
differenzierbar ist, gilt dort
![]() .
.
Da ![]() in
in ![]() links- wie rechtsseitig einen Grenzwert besitzt, nämlich
links- wie rechtsseitig einen Grenzwert besitzt, nämlich
![]() und
und
![]() , und dort auch links- und
rechtsseitig differenzierbar ist, gilt dort
, und dort auch links- und
rechtsseitig differenzierbar ist, gilt dort
![]() .
.
siehe auch:
| automatisch erstellt am 11. 8. 2006 |