Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Fourierentwicklung für die Bestimmung des Wertes einer Reihe

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Berechne die Fourierreihe der $ \pi$ -periodischen Funktion $ f:\mathbb{R}\to\mathbb{R}$ , welche durch $ f(x)=e^x$ für $ x\in [0,\pi)$ gegeben ist.

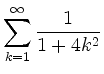Vergleiche $ f$ mit $ \mathrm{S}_f(x)$ . Setze beidseitig $ x = 0$ ein, um $ \displaystyle\sum_{k = 1}^\infty \frac{1}{1 + 4k^2}$ zu berechnen.

Lösung.

Eine direkte Berechnung der reellen Fourierkoeffizienten wäre aufwendiger als die nun durchzuführende Berechnung der komplexen Fourierkoeffizienten von $ f$ . Es ist

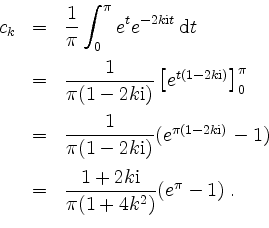
\begin{displaymath} \begin{array}{rcl} c_k & = & \dfrac{1}{\pi}\displaystyle\... ...2k\mathrm{i}}{\pi(1 + 4k^2)} (e^\pi - 1) \; .\\ \end{array} \end{displaymath}

für $ k\in\mathbb{Z}$ . Somit ist

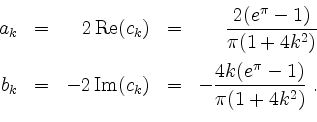
\begin{displaymath} \begin{array}{rcrcr} a_k & = & 2\operatorname{Re }(c_k) & ... ...& -\dfrac{4k(e^\pi - 1)}{\pi(1 + 4k^2)} \; . \\ \end{array} \end{displaymath}

Wir erhalten

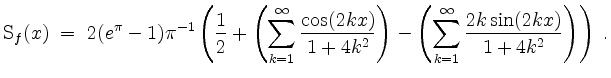
$\displaystyle \mathrm{S}_f(x) \;=\; 2(e^\pi - 1)\pi^{-1} \left(\frac{1}{2} + \l... ... - \left(\sum_{k = 1}^\infty \frac{2k\sin(2kx)}{1 + 4k^2}\right)\right) \; . $

Skizze des Graphen der jeweils ersten $ 3$ und des Graphen der jeweils ersten $ 100$ Summanden der Fourierreihe.

Da $ f$ für $ x\in (0,\pi)$ differenzierbar ist, gilt dort $ \mathrm{S}_f(x) = f(x)$ .

Bei $ x = 0$ ist $ f$ noch einseitig stetig und einseitig differenzierbar mit $ f(0+) = 1$ und $ f(0-) = e^\pi$ . Also gilt dort

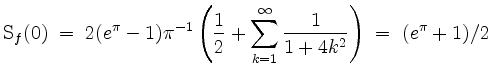
$\displaystyle \mathrm{S}_f(0) \;=\; 2(e^\pi - 1)\pi^{-1} \left(\frac{1}{2} + \sum_{k = 1}^\infty \frac{1}{1 + 4k^2}\right) \;=\; (e^\pi + 1)/2 $

und somit

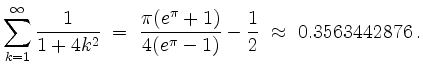
$\displaystyle \sum_{k = 1}^\infty \frac{1}{1 + 4k^2} \;=\; \dfrac{\pi(e^\pi + 1)}{4(e^\pi - 1)} - \dfrac{1}{2}\;\approx\; 0.3563442876 \; . $

(Autoren: Künzer/Martin/Tentler/Wahrheit)

siehe auch:

  automatisch erstellt am 22.  8. 2006