Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Stetigkeitsuntersuchung mit den Parsevalschen Gleichungen

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Konvergiert

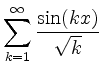
$\displaystyle \sum_{k = 1}^\infty \frac{\sin(kx)}{\sqrt k} $

gegen eine Funktion in $ x$ , die in $ [-\pi,\pi]$ nur endlich viele Unstetigkeitsstellen hat, und für die ferner in jeder solchen Unstetigkeitsstelle der links- und der rechtsseitige Grenzwert existieren?

Lösung.

Wäre die angegebene Reihe eine Funktion wie angegeben, so wäre

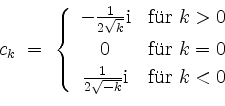
\begin{displaymath} c_k \;=\; \left\{ \begin{array}{cl} -\frac{1}{2\sqrt k}\mat... ...\sqrt{-k}}\mathrm{i} & \mbox{f''ur $k < 0$} \end{array}\right. \end{displaymath}

die Koeffizientenfolge $ (c_k)_{k\in\mathbb{Z}}$ der Fourierentwicklung einer stetigen Funktion.

Mit der Parsevalschen Normgleichung gäbe das die konvergente Reihe

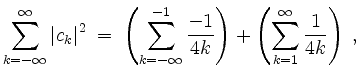
$\displaystyle \sum_{k = -\infty}^{\infty} \vert c_k\vert^2 \;=\; \left(\sum_{k ... ...} \frac{-1}{4k} \right) + \left(\sum_{k = 1}^{\infty} \frac{1}{4k} \right)\; , $

welche aber in beiden Bestandteilen divergiert. Das gibt uns einen Widerspruch.

Skizze des Graphen der ersten $ 5$ und des Graphen der ersten $ 100$ Summanden der angegebenen trigonometrischen Reihe.

\includegraphics[width = 12cm]{l1_par.eps}
(Autoren: Künzer/Martin/Tentler/Wahrheit)

siehe auch:

  automatisch erstellt am 11.  8. 2006