Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

System von linearen Differentialgleichungen bei diagonalisierbarer Matrix

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Es sei $ A \in \mathbb{C}^{n \times n}$ eine diagonalisierbare Matrix, d.h. es gebe eine reguläre Matrix $ S \in \mathbb{C}^{n \times n}$ so, daß

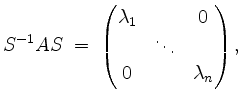
$\displaystyle S^{-1} A S \; =\; \begin{pmatrix} \lambda_1 & & 0\\ & \ddots &\\ 0 & & \lambda_n \end{pmatrix}, $

wobei auf der Diagonalen die Eigenwerte $ \lambda_1, \ldots, \lambda_n$ der Matrix $ A$ stehen.

Zeige, daß in diesem Fall

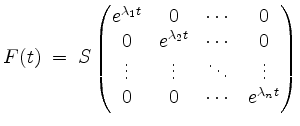
$\displaystyle F(t) \; =\; S \begin{pmatrix} e^{\lambda_1 t} & 0 & \cdots & 0\\ ... ...s & \vdots & \ddots & \vdots\\ 0 & 0 & \cdots & e^{\lambda_n t} \end{pmatrix}$

eine Fundamentalmatrix des homogenen linearen Systems von Differentialgleichungen mit konstanten Koeffizienten

$\displaystyle \dot y \; =\; A y $

ist.

Lösung.

Die gegebene Diagonalmatrix

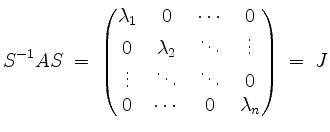
$\displaystyle S^{-1} A S \; =\; \begin{pmatrix} \lambda_1 & 0 & \cdots & 0\\ 0... ...& \ddots & \ddots & 0\\ 0 & \cdots & 0 & \lambda_n \\ \end{pmatrix} \; =\; J $

ist in Jordanform. Damit ist also ein Fundamentalmatrix der Differentialgleichung gegeben durch

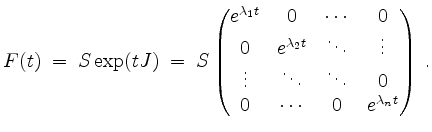
$\displaystyle F(t) \; =\; S \, \mathrm{exp}(tJ) \; =\; S \begin{pmatrix} e^{\la... ... & \ddots & \ddots & 0 \\ 0 & \cdots & 0 & e^{\lambda_n t} \end{pmatrix} \; . $

Diesen Umstand kann man sich alternativ auch leicht wie folgt erklären.

Substituiert man $ y = S z$ , bzw. $ z = S^{-1} y$ , so führt das gegebene System $ \dot y = A y$ auf das System $ (S\dot z) = A (S z)$ , d.h. auf das System

$\displaystyle \dot z = \mathrm{diag}(\lambda_1, \, \ldots, \, \lambda_n) z $

bzw.

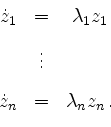
\begin{displaymath} \begin{array}{ccc} \dot z_1 & = & \lambda_1 z_1\vspace{3mm}\... ...s & \vspace{3mm}\\ \dot z_n & = & \lambda_n z_n\,. \end{array}\end{displaymath}

Zu diesem System ist eine Fundamentalmatrix leicht auffindbar, nämlich

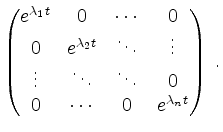
$\displaystyle \begin{pmatrix} e^{\lambda_1 t} & 0 & \cdots & 0\\ 0 & e^{\lambd... ...s & \ddots & \ddots & 0\\ 0 & \cdots & 0 & e^{\lambda_n t} \end{pmatrix} \; . $

Die Resubstitution $ y = S z$ führt schließlich auf die gewünschte Behauptung.

(Autoren: Künzer/Martin/Tentler/Wahrheit)

siehe auch:

  automatisch erstellt am 11.  8. 2006