Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Ein System von linearen Differentialgleichungen mit Anfangswertproblem

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

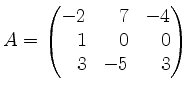Sei $ A=\begin{pmatrix}-2&\hfill 7&-4\\ \hfill 1&\hfill 0&\hfill 0\\ \hfill 3&-5&\hfill 3\end{pmatrix}\,$ .

1.
Berechne alle Lösungen von $ x'(t)=Ax(t)\,$ .
2.
Löse das Anfangswertproblem $ x'(t)=Ax(t)\,$ mit $ x(0)=(1,1,0)^\mathrm{t}\,$ .
3.
Berechne alle Lösungen von $ x'(t)=Ax(t)+b(t)\,$ mit $ b(t)=(2\sin t,\sin t,0)^\mathrm{t}\,$ .

Lösung.

1.
Zunächst berechnen wir das charakteristische Polynom

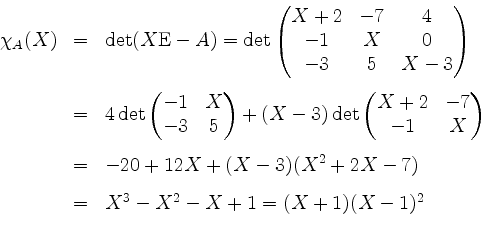
\begin{displaymath} \begin{array}{rcl} \chi_A(X)&=&\det(X\mathrm{E}-A)=\det\begi... ...^2+2X-7)\vspace{3mm}\\ &=&X^3-X^2-X+1=(X+1)(X-1)^2 \end{array}\end{displaymath}

Also hat $ A$ die Eigenwerte $ -1$ und $ 1$ . Wir berechnen nun die Jordanform von $ A$ mit einer Transformationsmatrix $ S=(s_1,s_2,s_3)$ . Für den Eigenwert $ -1$ setzen wir $ C_1:=A+\mathrm{E}$ und erhalten sofort

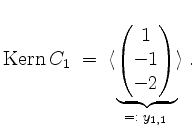
$\displaystyle \operatorname{Kern }C_1 \; =\; \langle\underbrace{\begin{pmatrix}1\\ -1\\ -2\end{pmatrix}}_{=:\; y_{1,1}}\rangle\; . $

Dies ist eine Basis des Hauptraums $ \mathrm{H}_A(-1)$ , also wählen wir $ s_1:=y_{1,1}$ .

Für den Eigenwert $ 1$ setzen wir $ C_2:=A-\mathrm{E}$ und berechnen

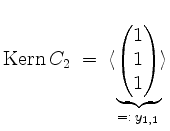
$\displaystyle \operatorname{Kern }C_2 \; =\; \langle\underbrace{\begin{pmatrix}1\\ 1\\ 1\end{pmatrix}}_{=:\; y_{1,1}}\rangle $

sowie

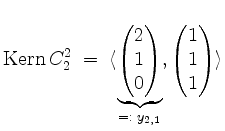
$\displaystyle \operatorname{Kern }C_2^2\; =\; \langle\underbrace{\begin{pmatrix... ...\\ 0\end{pmatrix}}_{=:\; y_{2,1}},\begin{pmatrix}1\\ 1\\ 1\end{pmatrix}\rangle $

woraus wir eine Basis $ (y_{1,1},y_{2,1})$ des Hauptraums $ \mathrm{H}_A(1)$ erhalten.

Wir ersetzen nun im nächsten Schritt diese Basis durch die einzige hier erforderliche Kette $ (s_2, s_3) := (C_2 y_{2,1}, y_{2,1})$ , welche ebenfalls eine Basis des Hauptraums $ \mathrm{H}_A(1)$ darstellt. (Daß $ C_2 y_{2,1} = y_{1,1}$ ist, darf als Zufall angesehen werden.) Insgesamt erhalten wir

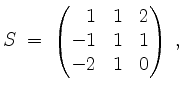
$\displaystyle S \; =\; \begin{pmatrix}\hfill 1&1&2\\ -1&1&1\\ -2&1&0\end{pmatrix}\; , $

und es ist

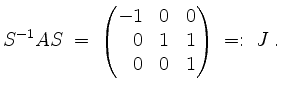
$\displaystyle S^{-1}AS\; =\;\begin{pmatrix}-1&\hfill 0&\hfill 0\\ \hfill 0&\hfill 1&\hfill 1\\ \hfill 0&\hfill 0&\hfill 1\end{pmatrix}\; =:\; J\;. $

Dann ist also

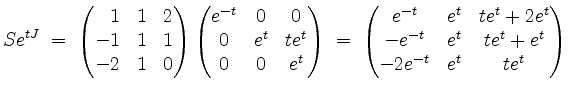
$\displaystyle Se^{tJ} \; =\; \begin{pmatrix}\hfill 1&1&2\\ -1&1&1\\ -2&1&0\end{... ...}e^{-t}&e^t&te^t+2e^t\\ -e^{-t}&e^t&te^t+e^t\\ -2e^{-t}&e^t&te^t\end{pmatrix} $

eine Fundamentalmatrix, so daß die allgemeine Lösung der Differentialgleichung die Gestalt

$\displaystyle x(t)\; =\; Se^{tJ}v $

hat, mit einem Vektor $ v\in\mathbb{C}^3\,$ .

2.
Wir lösen nun die Differentialgleichung mit dem Anfangswert $ x(0)=(1,1,0)^\mathrm{t}$ . Aus 1. erhalten wir mit $ v=(v_1,v_2,v_3)^\mathrm{t}$ den Ansatz

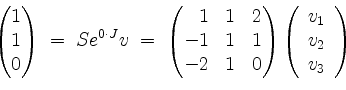
\begin{displaymath} \begin{pmatrix}1\\ 1\\ 0\end{pmatrix}\; =\; Se^{0\cdot J}v \... ...t( \begin{array}{l} v_1 \\ v_2 \\ v_3 \\ \end{array}\right) \end{displaymath}

und daraus die eindeutige Lösung

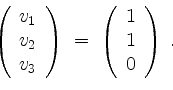
\begin{displaymath} \left( \begin{array}{l} v_1 \\ v_2 \\ v_3 \\ \end{array}\... ...eft( \begin{array}{l} 1 \\ 1 \\ 0 \\ \end{array}\right)\; . \end{displaymath}

Somit ist

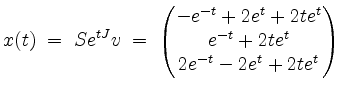
$\displaystyle x(t)\; =\; Se^{tJ}v \; =\; \begin{pmatrix}-e^{-t}+2e^t+2te^t\\ e^{-t}+2te^t\\ 2e^{-t}-2e^t+2te^t \end{pmatrix}$

die eindeutige Lösung des gegebenen Anfangswertproblems.

3.
Um nun das inhomogene System zu lösen, verwenden wir die Methode der Variation der Konstanten. Wir suchen $ x$ von der Form

$\displaystyle x(t)\; =\; Se^{tJ}v(t) $

mit einem noch zu bestimmenden $ v$ . Einsetzen in $ x' = Ax + b$ liefert die Bedingung

$\displaystyle v'(t)\; =\; e^{-tJ}S^{-1}b(t)\; . $

Wir berechnen zunächst $ S^{-1}$ mit einer (leicht variierten) Anwendung des Gaußalgorithmus.

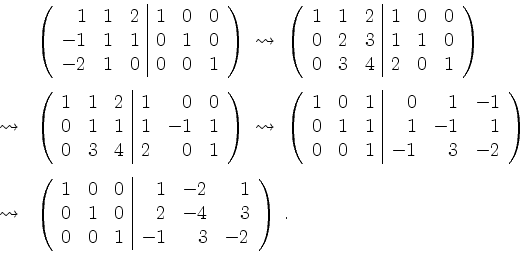
\begin{displaymath} \begin{array}{rl} & \left( \begin{array}{rrr\vert rrr} 1 & 1... ... 0 & 1 & -1 & 3 & -2 \\ \end{array}\right)\; . \\ \end{array}\end{displaymath}

Also ist

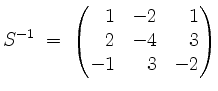
$\displaystyle S^{-1}\; =\; \begin{pmatrix}\hfill 1&-2&\hfill 1\\ \hfill 2&-4&\hfill 3\\ -1&\hfill 3&-2\end{pmatrix}$

und

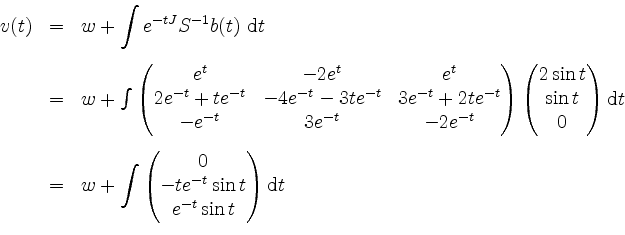
\begin{displaymath} \begin{array}{rcl} v(t) & = & w+\displaystyle\int e^{-tJ}S^{... ...e^{-t}\sin t\\ e^{-t}\sin t\end{pmatrix}\mathrm{d}t \end{array}\end{displaymath}

mit einem konstanten Vektor $ w\in\mathbb{C}^3$ . Durch komplexe Interpretation von Sinus und Cosinus oder auch durch zweifache partielle Integration erhält man

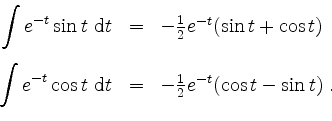
\begin{displaymath} \begin{array}{rcl} \displaystyle\int e^{-t}\sin t\ \mathrm{d... ...\mathrm{d}t&=&-\frac{1}{2}e^{-t}(\cos t-\sin t)\; . \end{array}\end{displaymath}

Daraus erhält man mit partieller Integration

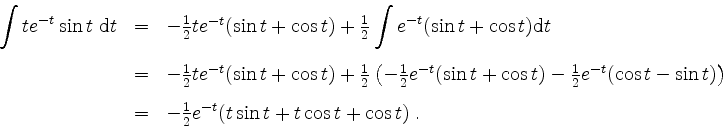
\begin{displaymath} \begin{array}{rcl} \displaystyle\int te^{-t}\sin t\ \mathrm{... ... &=&-\frac{1}{2}e^{-t}(t\sin t+t\cos t+\cos t)\; . \end{array}\end{displaymath}

Somit ist

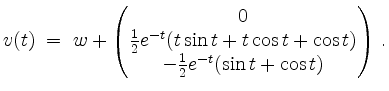
$\displaystyle v(t)\; =\; w + \begin{pmatrix}0\\ \frac{1}{2}e^{-t}(t\sin t+t\cos t+\cos t)\\ -\frac{1}{2}e^{-t}(\sin t+\cos t)\end{pmatrix}\,. $

Die allgemeine Lösung ist demnach

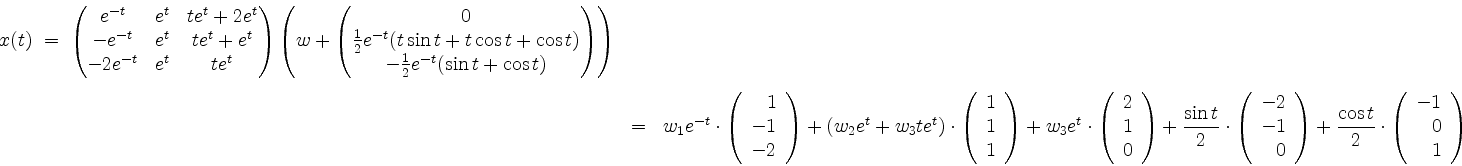
\begin{displaymath} \begin{array}{rcl} x(t)\; =\; \begin{pmatrix}e^{-t}&e^t&te^t... ...ay}{r} -1 \\ 0 \\ 1 \\ \end{array}\right) \\ \end{array}\end{displaymath}

mit einem Vektor $ w = (w_1,w_2,w_3)^\mathrm{t}\in\mathbb{C}^3$ .
(Autoren: Künzer/Martin/Tentler/Wahrheit)

siehe auch:

  automatisch erstellt am 22.  8. 2006