Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Ein homogenes lineares System von Differentialgleichungen

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

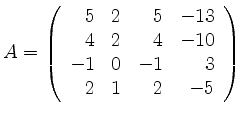Sei $ A=\left(\begin{array}{rrrr} 5& 2& 5&-13\\ 4& 2& 4&-10\\ -1& 0&-1& 3\\ 2& 1& 2&-5\end{array}\right)$ .

Berechne alle Lösungen von $ x'(t) = Ax(t)\, $ .

Lösung.

Das charakteristische Polynom von $ A$ ist

$\displaystyle \chi_A(X)=X^3(X-1)\,,$

also hat $ A$ die Eigenwerte $ 0\,$ und $ \,1\,$ . Wir berechnen nun die Jordanform von $ A$ mit einer Transformationsmatrix $ S=(s_1,s_2,s_3,s_4)$ .

Für den Eigenwert 0 setzen wir $ C_1:=A - 0\cdot\mathrm{E}$ und berechnen

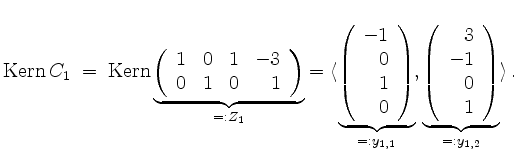
$\displaystyle \operatorname{Kern }C_1\; =\; \operatorname{Kern }\underbrace{\l... ...e{\left(\begin{array}{r}3\\ -1\\ 0\\ 1\end{array}\right)}_{=:y_{1,2}}\rangle\,.$

Außerdem ist

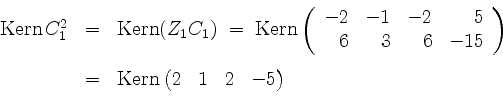
\begin{displaymath} \begin{array}{rcl} \operatorname{Kern }C_1^2&=&\operatorname... ...ratorname{Kern }\begin{pmatrix}2&1&2&-5\end{pmatrix}\end{array}\end{displaymath}

und wir ergänzen $ (y_{1,1},y_{2,1})$ mit $ y_{2,1}:=(-1,2,0,0)^\mathrm{t}\in\operatorname{Kern }C_1^2$ zu einer Basis $ (y_{1,1},y_{1,2},y_{2,1})$ von $ \operatorname{Kern }C_1^2$ , die auch Basis des Hauptraums $ \mathrm{H}_A(0)$ ist. Nun ergänzen wir $ C_1 y_{2,1}$ mit $ y_{1,2}$ zu einer Basis $ (C_1 y_{2,1},y_{1,2})$ von $ \operatorname{Kern }C_1$ und setzen $ (s_1,s_2,s_3):=(C_1y_{2,1},y_{2,1},y_{1,2})\,$ .

Für den Eigenwert $ 1$ setzen wir $ C_2:=A-E$ und erhalten

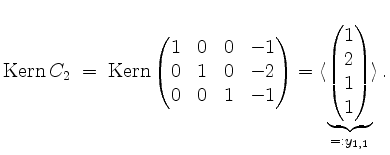
$\displaystyle \operatorname{Kern }C_2 \; =\; \operatorname{Kern }\begin{pmatrix... ...le\underbrace{\begin{pmatrix}1\\ 2\\ 1\\ 1\end{pmatrix}}_{=:y_{1,1}}\rangle\,. $

Dies ist eine Basis des Hauptraums $ \mathrm{H}_A(1)$ , also wählen wir $ s_4:=y_{1,1}$ .

Mit

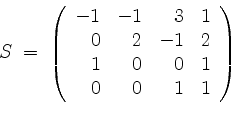
\begin{displaymath} S \; =\; \left( \begin{array}{rrrr} -1 & -1 & 3 & 1 \\ 0 ... ...2 \\ 1 & 0 & 0 & 1 \\ 0 & 0 & 1 & 1 \\ \end{array}\right) \end{displaymath}

gilt also nun

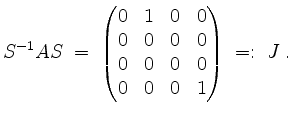
$\displaystyle S^{-1}AS\; =\; \begin{pmatrix}0&1&0&0\\ 0&0&0&0\\ 0&0&0&0\\ 0&0&0&1\end{pmatrix} \; =:\; J \; . $

Somit erhalten wir

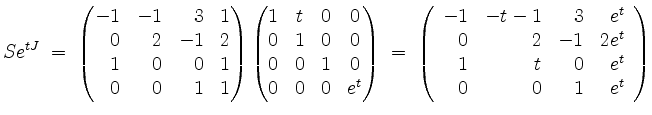
$\displaystyle Se^{tJ} \; =\; \begin{pmatrix}-1&-1&\hfill 3&\hfill 1\\ \hfill 0&... ...ay}{rrrr}-1&-t-1&3&e^t\\ 0&2&-1&2e^t\\ 1&t&0&e^t\\ 0&0&1&e^t\end{array}\right) $

eine Fundamentalmatrix, so daß die allgemeine Lösung der Differentialgleichung

$\displaystyle x(t)\; =\; Se^{tJ}c $

mit einem Vektor $ c\in\mathbb{C}^4\,$ lautet.
(Autoren: Künzer/Martin/Tentler/Wahrheit)

siehe auch:

  automatisch erstellt am 22.  8. 2006