Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Beispiel: Wurzelgleichung

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Das rechnerische Lösen von Gleichungen in denen Wurzeln vorkommen ist im Allgemeinen nicht möglich. In einfachen Fällen kann eine Wurzelgleichung aber durch geeignetes Potenzieren gelöst werden. Dabei muss zunächst die Wurzel auf einer Seite der Gleichung isoliert werden. Dann kann die Gleichung potenziert und gelöst werden. Bei den Lösungen die man so erhält ist aber Vorsicht geboten, da die potenzierte Gleichung in der Regel auch Lösungen besitzt die die ursprüngliche Gleichung nicht lösen. Das Potenzieren ist also keine Äquivalenzumformung. Es gilt aber, dass jede Lösung der ursprünglichen Gleichung auch die potenzierte Gleichung löst.

Beispielsweise sollen die Lösungen der Gleichung

$\displaystyle \sqrt{4+x^2}-1=x $

gesucht werden. Isolieren der Wurzel liefert

$\displaystyle \sqrt{4+x^2}=x+1 \,. $

Durch Quadrieren erhält man

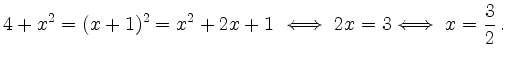
$\displaystyle 4+x^2=(x+1)^2=x^2+2x+1 \ \Longleftrightarrow \ 2x=3 \Longleftrightarrow \ x=\frac32 \,. $

Setzt man die Lösungen in die ursprüngliche Gleichung ein, erhält man

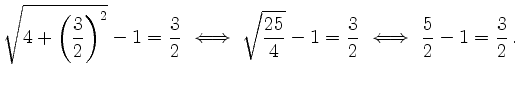
$\displaystyle \sqrt{4+\left(\frac32\right)^2}-1=\frac32 \ \Longleftrightarrow \ \sqrt{\frac{25}{4}}-1=\frac32 \ \Longleftrightarrow \ \frac52-1=\frac32 \,. $

Die Lösung der quadrierten Gleichung löst also auch die Wurzelgleichung.

Anders ist das bei der Gleichung

$\displaystyle \sqrt{x^2} =-2 \,. $

Da die Wurzel einer Zahl immer positiv ist kann die Gleichung keine Lösung haben. Durch Quadrieren erhält man aber

$\displaystyle x^2=4 \,. $

Die quadrierte Form hat also die Lösungen $ x_{1,2}=\pm 2$. Beide Lösungen ergeben aber in die Wurzelgleichung eingesetzt einen Widerspruch.
(Autor: Vorkurs Mathematik)

siehe auch:

  automatisch erstellt am 23. 10. 2007