Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Beispiel: Bruchgleichung

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht
Um Gleichungen zu lösen in denen Brüche vorkommen, versucht man durch geschicktes Umformen die Bruchterme wegzubekommen. Dazu faktorisiert man zuerst die Nenner um die Definitionsmenge um den Hauptnenner zu bestimmen. Dann multipliziert man die ganze Gleichung mit dem Hauptnenner und löst die dabei entstehende Gleichung. Dabei muss man beachten, dass so eine Multiplikation keine Äquivalenzumformung ist. Also muss man am Ende immer nachprüfen, ob die erhaltenen Lösungen wirklich zur Definitionsmenge der Ausgangsgleichung gehören.

Als Beispiel wird die Bruchgleichung

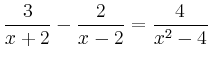
$\displaystyle \frac{3}{x+2} - \frac{2}{x-2} = \frac{4}{x^2-4} $

betrachtet.

Mit einer der binomischen Formeln kann man den Nenner auf der rechten Seite in Linearfaktoren zerlegen:

$\displaystyle x^2 - 4 = (x-2)(x+2). $

Also besteht die Definitionsmenge aus allen reellen Zahlen außer -2 und 2. Nun multipliziert man beide Seiten der Gleichung mit den Hauptnenner:

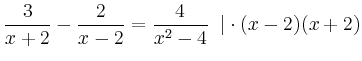
$\displaystyle \frac{3}{x+2} - \frac{2}{x-2} = \frac{4}{x^2-4} \;\; \vert \cdot(x-2)(x+2) $

$\displaystyle \Longrightarrow 3(x-2) - 2(x+2) = 4 \Longrightarrow x = 14. $

Wie man sieht, liegt das Ergebnis noch im Definitionsbereich und ist damit auch die Lösung der Ausgangsgleichung.

(Aus: Vorkurs Mathematik)

siehe auch:

  automatisch erstellt am 5. 10. 2012