Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Datenanalyse

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht
Datenanalyse für einen Vektor mit 7 Zufallszahlen: 
  >> data=rand(1,7)
  data =
      0.6400    0.2473    0.3527    0.1879    0.4906    0.4093    0.4635
  >> [max(data) min(data) mean(data) median(data)]
  ans =
      0.6400    0.1879    0.3988    0.4093
  >> sort(data)
  ans =
      0.1879    0.2473    0.3527    0.4093    0.4635    0.4906    0.6400
  >> diff(data)
  ans =
     -0.3927    0.1054   -0.1648    0.3028   -0.0814    0.0543
In der zweiten Eingabezeile wurden die Ergebnisse der Funktionen max, min, mean und median der Einfachheit halber in einem Vektor zusammengefasst.

Beim Befehl cumprod bzw. cumsum entspricht der $ i$-te Eintrag im Ergebnisvektor dem Produkt bzw. der Summe der Elemente 1 bis $ i$ im Parametervektor. Wendet man beispielsweise cumprod auf den Vektor mit den Elementen 1 bis 7 an, so erhält man einen Vektor mit den Elementen $ 1!=1$ bis $ 7!=5040$: 

  >> fakultaeten=cumprod(1:7)
  fakultaeten =
         1       2       6      24     120     720    5040

Polynome können mit Hilfe der MATLAB-Funktion conv bzw. deconv multipliziert bzw. dividiert werden. Zu übergeben sind dabei jeweils die Koeffizientenvektoren der Polynome. So steht beispielsweise 

  >> conv([1 -2 3],[2 1])
  ans =
       2    -3     4     3
für die Rechnung

$\displaystyle (x^2-2x+3)(2x+1)=2x^3-3x^2+4x+3 $

und 
  >> [q,r]=deconv([2 -3 4 3],[1 -2])
  q =
       2     1     6
  r =
       0     0     0    15
für die Rechnung

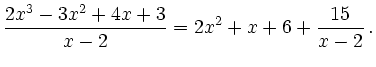
$\displaystyle \frac{2x^3-3x^2+4x+3}{x-2}=2x^2+x+6+\frac{15}{x-2} \,. $

(Autoren: Hörner/Wipper)
[Verweise]
  automatisch erstellt am 12.  1. 2007