Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Anfangswertproblem und Richtungsfeld

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht
Lösung der Differenzialgleichung

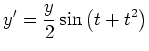
$\displaystyle y'=\frac{y}{2} \sin\left(t+t^2\right) $

für die Anfangswerte $ y(0)=1$ und $ y(0)=2$:

Auswertungs-Funktion odefun.m der rechten Seite: 

function ys=odefun(t,y)
ys=sin(t+t.^2).*y/2;

Visualisierung des Richtungsfeldes und der Lösungen der beiden Anfangswertprobleme für $ t\in [0,\pi]$: 

>> % Richtungsfeld plotten
>> [t,y]=meshgrid(linspace(0,pi,20),linspace(.5,3.5,20));
>> ys=odefun(t,y);
>> quiver(t,y,ones(size(ys)),ys);
>> hold on

>> % Anfangswertprobleme loesen
>> ode23(@odefun,[0,pi],1)  
>> ode45('odefun',[0,pi],2)

\includegraphics[width=.8\linewidth]{ode.eps}
(Autor: Wipper)

siehe auch:

  automatisch erstellt am 25.  1. 2006