Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Satz von Stokes bei einem Zylinder

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht
Als Beispiel wird der Fluss der Rotation des räumlichen Vektorfeldes

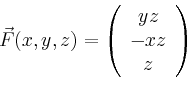
\begin{displaymath} \vec{F}(x,y,z)=\left( \begin{array}{c} yz\\ -xz\\ z\\ \end{array}\right) \end{displaymath}

nach außen durch den Zylindermantel

$\displaystyle S:\quad x^2+y^2 = 1,\quad 0\leq z \leq 1\,, $

betrachtet. Als Parametrisierung für die untere Randkurve $ C_u$ wird

\begin{displaymath} \vec{r}(t)=\left( \begin{array}{c} \cos t\\ \sin t \\ 0\\ \end{array}\right),\quad t\in[0,2\pi]\,, \end{displaymath}

verwendet. Entsprechend ist für die obere Randkurve $ C_o$

\begin{displaymath} \vec{r}(t)=\left( \begin{array}{c} \cos(-t)\\ \sin(-t) \\ 1\\ \end{array}\right),\quad t\in[0,2\pi]\,, \end{displaymath}

wobei die entgegengesetzte Orientierung zu berücksichtigen ist.

Der gesuchte Fluss ist nach dem Satz von Stokes gleich der Summe der Arbeitsintegrale über die beiden Randkurven,

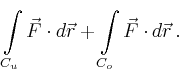
$\displaystyle \int\limits_{C_u} \vec{F} \cdot d\vec{r} + \int\limits_{C_o} \vec{F} \cdot d\vec{r} \,. $

Mit

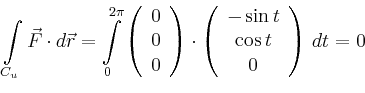
\begin{displaymath} \int\limits_{C_u} \vec{F} \cdot d\vec{r} = \int\limits_0^{... ...n{array}{c} -\sin t\\ \cos t \\ 0\\ \end{array}\right)\,dt =0 \end{displaymath}

und

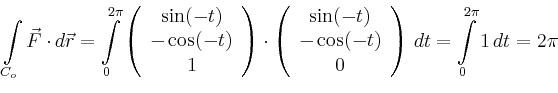
\begin{displaymath} \int\limits_{C_o} \vec{F} \cdot d\vec{r} = \int\limits_0^{... ... \end{array}\right)\,dt = \int\limits_0^{2\pi} 1 \, dt = 2\pi \end{displaymath}

ist der Fluss durch den Mantel also $ 2\pi$.

Alternativ kann der Fluss durch den Mantel auch mit Hilfe der Flüsse durch Deckel und Boden des Zylinders berechnet werden. Da für diese Flächen die Normale parallel zur $ z$-Achse ist, muss nur die $ z$-Komponente der Rotation von $ \vec{F}$ bestimmt werden:

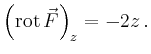
$\displaystyle \left(\operatorname{rot} \vec{F}\right)_z = -2z\,. $

Damit ist der Fluss durch den Boden ($ z=0$) null, und der Fluss durch den Deckel ($ z=1$) entspricht dem $ (-2)$-fachen der Kreisfläche, also $ -2\pi$. Da der Gesamtfluss durch den Zylinder verschwindet ( div rot $ \vec{F} =0$), ist der Fluss durch den Mantel $ 2\pi$.
[Verweise]
  automatisch erstellt am 9. 10. 2013