Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] Englische Flagge
Mathematik-Online-Lexikon:

Vektoren im Dreidimensionalen

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht
Wie im Zweidimensionalen sind zwei Vektoren im $ \mathbb{R}^3$ linear abhängig, wenn sie parallel sind, d.h. wenn ein Vektor ein Vielfaches des anderen ist.

Drei Vektoren sind linear abhängig, wenn zwei Vektoren parallel sind oder wenn ein Vektor in der von den beiden anderen Vektoren aufgespannten Ebene liegt. Beispielsweise gilt für

$\displaystyle u = (1,2,-3)^{\operatorname t},\,v = (4,-6,2)^{\operatorname t},\,w = (-9,3,6)^{\operatorname t} $

$ 6u + 3v + 2w = (0,0,0)^{\operatorname t}$; die Vektoren sind also linear abhängig.

Definitionsgemäß ist der Test für lineare Abhängigkeit äquivalent zu einem homogenen linearen Gleichungssystem

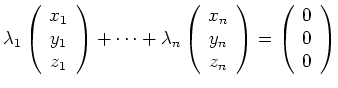
$\displaystyle \lambda_1 \left(\begin{array}{c} x_1 \\ y_1 \\ z_1 \end{arra... ...d{array}\right) = \left(\begin{array}{c} 0 \\ 0 \\ 0 \end{array}\right) $

für die Skalare $ \lambda_i$. Dies zeigt insbesondere, dass vier Vektoren im $ \mathbb{R}^3$ immer linear abhängig sind.
(Autoren: App/Höllig)

siehe auch:

  automatisch erstellt am 25.  1. 2006