Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Moivre-Laplace

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Wie oft muß eine Münze geworfen werden, damit die relative Häufigkeit des Wurfs Zahl (also die Anzahl der erfolgreichen geteilt durch die Anzahl aller Würfe) mit einer Wahrscheinlichkeit von mindestens $ \mbox{$0.95$}$ im Intervall $ \mbox{$[0.48,0.52]$}$ liegt? Berechne eine Näherungslösung mit Hilfe des Grenzwertsatzes von de Moivre-Laplace.

Die Folge der Zufallsvariablen $ \mbox{$(X_n)_{\mathbb{N}}$}$, die den Münzwurf beschreibt ( $ \mbox{$X_n = 1 : \text{ Zahl im }n\text{-ten Wurf}$}$, $ \mbox{$X_n = 0 : \text{eine R\uml uckseite im }n\text{-ten Wurf}$}$) ist unabhängig, und es gilt $ \mbox{$P(X_n = 0)= 0.5$}$ und $ \mbox{$P(X_n = 1) = 0.5$}$ für alle $ \mbox{$n\in\mathbb{N}$}$.

Wir hatten mit $ \mbox{$\bar{X}_n := \frac{1}{n}\sum_{k=1}^n X_k$}$ den Mittelwert der ersten $ \mbox{$n$}$ Würfe bezeichnet. Es ist

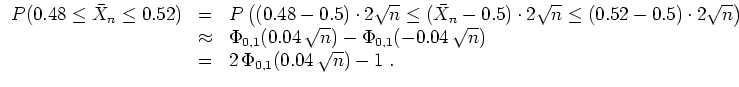
$ \mbox{$\displaystyle \begin{array}{rcl} P(0.48 \leq \bar{X}_n \leq 0.52) &=... ...(-0.04\,\sqrt{n})\\ &=& 2\,\Phi_{0,1}(0.04\,\sqrt{n}) - 1\; . \end{array}$}$

Gefragt ist $ \mbox{$n\in\mathbb{N}$}$ mit

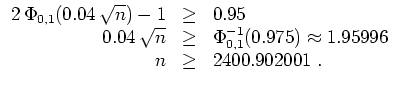
$ \mbox{$\displaystyle \begin{array}{rcl} 2\,\Phi_{0,1}(0.04\,\sqrt{n})-1 & \g... ...{-1}(0.975) \approx 1.95996 \\ n & \geq & 2400.902001\; . \\ \end{array}$}$
Der Wert für $ \mbox{$\Phi_{0,1}^{-1}(0.975)$}$ wird aus einer Tabelle entnommen.

Die Münze muß somit mindestens $ \mbox{$2401$}$-mal geworfen werden.

(Autoren: Künzer/Meister/Nebe)

siehe auch:

  automatisch erstellt am 25.  1. 2006