Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Approximation (Poisson-Verteilung)

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Mit einer Wahrscheinlichkeit von $ \mbox{$p=0.975$}$ verschmäht Kasper die Suppe in der Mensa. Wie groß ist die Wahrscheinlichkeit, daß Kasper in einem Semester (à $ \mbox{$80$}$ Tage) fünf Suppen gegessen hat? Berechne zuerst den genauen Wert und approximiere dann mit der Poissonverteilung.

Die Wahrscheinlichkeit, daß Kasper eine Suppe ißt, ist $ \mbox{$p = \frac{1}{40}$}$. Die exakte Wahrscheinlichkeit für fünf Suppen im Semester ist also

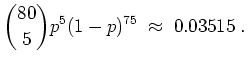
$ \mbox{$\displaystyle \binom{80}{5} p^5 (1-p)^{75} \;\approx\; 0.03515\; . $}$
Unter Verwendung der Poissonapproximation mit dem Parameter $ \mbox{$\lambda = 80p = 2$}$ beträgt die Wahrscheinlichkeit, fünf Suppen gegessen zu haben,
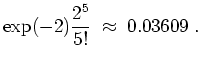
$ \mbox{$\displaystyle \exp(-2) \frac{2^5}{5!} \;\approx\; 0.03609\; . $}$

(Autoren: Künzer/Meister/Nebe)
[Verweise]
  automatisch erstellt am 25.  1. 2006