Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] Englische Flagge
Mathematik-Online-Lexikon:

Kurvendiskussion einer rationalen Funktion

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht
Es wird eine Funktionsuntersuchung für die Funktion

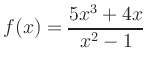
$\displaystyle f(x)=\frac{5x^3+4x}{x^2-1} $

durchgeführt.

Symmetrie: Der Zähler ist ungerade und der Nenner gerade. Die Funktion ist also ungerade, d.h. punktsymmetrisch zum Ursprung.

Periodizität: Die Funktion ist nicht periodisch.

Unstetigkeitsstellen und Polstellen: Der Nenner besitzt bei $ x=\pm 1$ einfache Nullstellen. Da der Zähler an diesen Punkten nicht Null ist, sind die Definitionslücken nicht hebbar, und $ -1$ und $ 1$ sind einfache Polstellen.

Nullstellen: Der Zähler verschwindet für $ x=0$.

Extrema: Die Ableitung

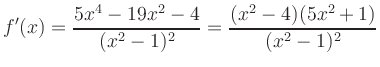
$\displaystyle f^\prime(x) = \frac{5x^4-19x^2-4}{(x^2-1)^2} = \frac{(x^2-4)(5x^2+1)}{(x^2-1)^2} $

verschwindet bei $ x = \pm 2$. Der Typ dieser kritischen Punkte kann aus dem qualitativen Verhalten von $ f$ gefolgert werden. Zunächst besitzt $ f$ wegen der einfachen Polstellen, an denen das Vorzeichen wechselt, keine globalen Extrema. Da $ f(x)\to-\infty$ für $ x\to -\infty$ und $ x\to -1$, muss das Intervall $ \left(-\infty,-1 \right)$ ein lokales Maximum enthalten. Analog enthält $ \left( 1, \infty \right)$ mindestens ein lokales Minimum. Zu den beiden einzigen Nullstellen der Ableitung erhält man also ein lokales Maximum bei $ (-2,-4/5)$ und ein lokales Minimum bei $ (2,4/5)$.

Wendepunkte: Die zweite Ableitung

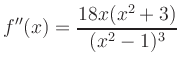
$\displaystyle f^{\prime\prime}(x) = \frac{18x(x^2+3)}{(x^2-1)^3} $

wechselt an der einzigen Nullstelle $ x=0$ das Vorzeichen; folglich ist $ (0,0)$ ein Wendepunkt.

Asymptoten: Mit Polynomdivision erhält man

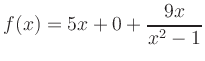
$\displaystyle f(x) = 5x + 0 + \frac{9x}{x^2-1} $

und somit $ p(x)=5x$ als Asymptote.

\includegraphics[width=10.4cm]{Kurvendiskussion_2}

siehe auch:

  automatisch erstellt am 6. 12. 2016