
Mathematik-Online-Lexikon:

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online-Lexikon: | |
Binomialverteilung |
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z | Übersicht |
Bei einer Lieferung von
![]() Computern funktioniert ein Computer nicht. Die
drei in Frage kommenden Produktionsanlagen haben die Ausschußanteile
von
Computern funktioniert ein Computer nicht. Die
drei in Frage kommenden Produktionsanlagen haben die Ausschußanteile
von
![]() ,
,
![]() und
und
![]() .
Bestimme mit Hilfe der Maximum-Likelihood-Methode, woher die Rechner kommen.
.
Bestimme mit Hilfe der Maximum-Likelihood-Methode, woher die Rechner kommen.
Die Ausschußverteilung ist also binomialverteilt mit Parameter
![]() ,
was besagt, daß
,
was besagt, daß
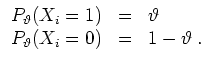
Hierzu die Likelihood-Funktion nur an der vorgebenen Stelle zu maximieren.
Die Likelihood-Funktion ist mit
![]() gegeben durch
gegeben durch
|
|
|
|
| 1 | 0.05 | 0.028 |
| 2 | 0.10 | 0.031 |
| 3 | 0.15 | 0.025 |
Nach der Maximum-Likelihood-Methode stammen die Rechner von Fabrik Nummer zwei.
siehe auch:
| automatisch erstellt am 25. 1. 2006 |