Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

rotierendes Seil

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Ein Seil der Länge $ \mbox{$l$}$, das in zwei Punkten $ \mbox{$x_0$}$, $ \mbox{$x_1$}$ der $ \mbox{$x$}$-Achse im schwerelosen Raum befestigt ist, rotiere mit Winkelgeschwindigkeit $ \mbox{$\omega$}$ um die $ \mbox{$x$}$-Achse. Gib eine Funktion $ \mbox{$y$}$ an, die den Achsabstand beschreibt.

Ein Massenpunkt des Seils mit Masse $ \mbox{$m$}$ hat die kinetische Energie $ \mbox{$\frac{1}{2} m (\omega y)^2$}$. Die gesamte kinetische Energie des Seils ist also $ \mbox{$\frac{m\omega^2}{2}\int_{x_0}^{x_1} y^2\sqrt{1+(y')^2}\, dx$}$. Gesucht sind die Extremalen von

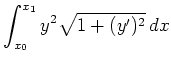
$ \mbox{$\displaystyle \int_{x_0}^{x_1} y^2\sqrt{1+(y')^2}\, dx $}$
unter der Nebenbedingung
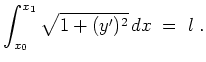
$ \mbox{$\displaystyle \int_{x_0}^{x_1} \sqrt{1+(y')^2}\, dx \; =\; l\; . $}$

Stelle die Euler-Lagrange-Differentialgleichung mit Lagrange-Multiplikator $ \mbox{$\lambda$}$ auf. (Diese ist leider nicht geschlossen lösbar.)

Da $ \mbox{$F(x,y,y') = F(y,y') = y^2\sqrt{1+(y')^2}$}$ und $ \mbox{$G(x,y,y')=G(y') = \sqrt{1+(y')^2}$}$ nicht explizit von $ \mbox{$x$}$ abhängen, gilt mit einem Lagrange-Multiplikator $ \mbox{$\lambda$}$ für $ \mbox{$\ L = F + \lambda G$}$ die Euler-Lagrange-Bedingung in der Form

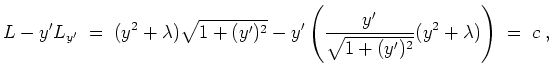
$ \mbox{$\displaystyle L-y'L_{y'} \; =\; (y^2 + \lambda)\sqrt{1+(y')^2} - y'\left(\frac{y'}{\sqrt{1+(y')^2}} (y^2 + \lambda)\right) \; =\; c \;, $}$
wobei $ \mbox{$c\in\mathbb{R}$}$ noch zu bestimmen ist.

Aus

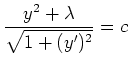
$ \mbox{$\displaystyle \frac{y^2+\lambda}{\sqrt{1+(y')^2}} = c $}$
und den Randbedingungen $ \mbox{$y(x_0) = 0$}$, $ \mbox{$y(x_1) = 0$}$ ist $ \mbox{$y$}$ zu bestimmen. Dies führt auf
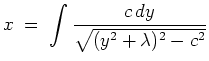
$ \mbox{$\displaystyle x \; =\; \int\frac{c\, dy}{\sqrt{(y^2 + \lambda)^2 - c^2}} $}$

Numerisch ergibt sich zum Beispiel folgendes Bild. Die untere schwarze Kurve ist ein in der Schwerelosigkeit rotierendes Seil, die obere graue Kurve ist ein in der Schwerkraft hängendes Seil. Vgl. hierzu die Aufgabe zur Berechnung des letzteren. (Die Seile sind unterschiedlich lang, haben aber gleichen Durchhang.)

\includegraphics[width=10cm]{l1.eps}
(Autoren: Künzer/Meister/Nebe)
[Verweise]
  automatisch erstellt am 25.  1. 2006